(Solved): Sketch the graph and show all local extrema and inflection points. Absolute maxima: \( (-\sqrt{2},- ...

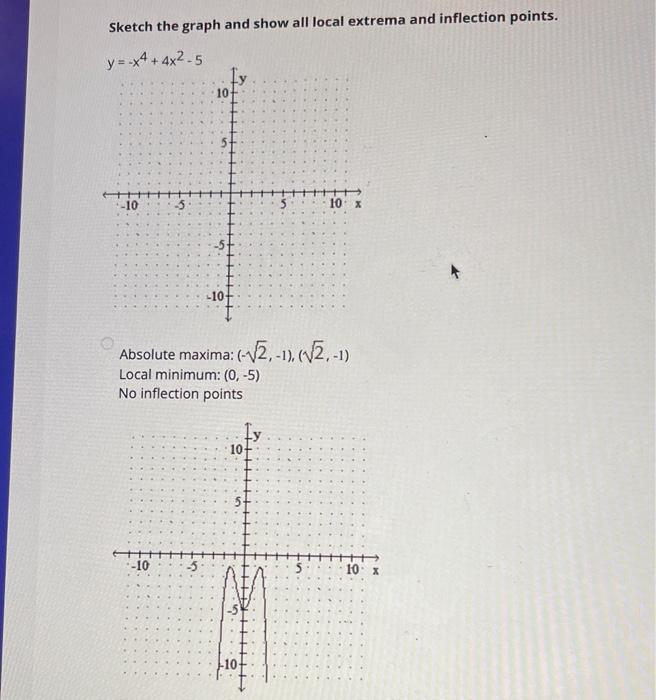
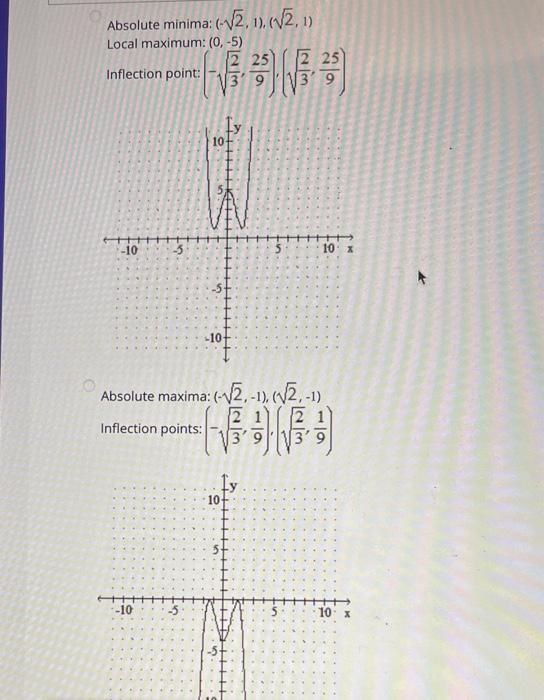
Sketch the graph and show all local extrema and inflection points. 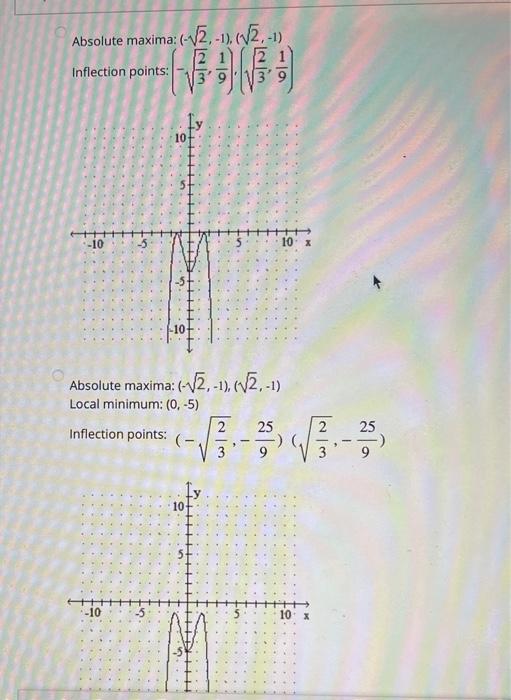Absolute maxima: \( (-\sqrt{2},-1),(\sqrt{2},-1) \) Local minimum: \( (0,-5) \) No inflection points Inflection point: \( \left(-\sqrt{\frac{2}{3}}, \frac{25}{9}\right),\left(\sqrt{\frac{2}{3}}, \frac{25}{9}\right) \) Absolute maxima: \( (-\sqrt{2},-1),(\sqrt{2},-1) \) Inflection points: \( \left(-\sqrt{\frac{2}{3}}, \frac{1}{9}\right),\left(\sqrt{\frac{2}{3}}, \frac{1}{9}\right) \) Absolute maxima: \( (-\sqrt{2},-1),(\sqrt{2},-1) \) Inflection points: \( \left(-\sqrt{\frac{2}{3}}, \frac{1}{9}\right),\left(\sqrt{\frac{2}{3}}, \frac{1}{9}\right) \) Absolute maxima: \( (-\sqrt{2},-1),(\sqrt{2},-1) \) Local minimum: \( (0,-5) \) Inflection points: \( \left(-\sqrt{\frac{2}{3}},-\frac{25}{9}\right)\left(\sqrt{\frac{2}{3}},-\frac{25}{9}\right) \)