(Solved): So FRUSTRATING! HELP! READ ALL ATTEMPTED CODE FIRST I am attempting to write code in Python to comp ...
So FRUSTRATING! HELP! READ ALL ATTEMPTED CODE FIRST
I am attempting to write code in Python to complete a RSA_Broadcast_Attack.
I have ATTEMPTED AND ADJUSTED 9 times now, and keep running into error
Code must be Python 3.10 and can only use standard libraries
NEEDS TO BE ABLE TO WORK WITH LARGE NUMBERS
VALIDATE SOLUTION WITH TEST CODE AT END - DO NOT PROVIDE AN ANSWER THAT FAILS TEST as WRONG ANSWER DOES NOT HELP
ATTEMPT 9 ANSWER I RECIEVED WITH CODE is at the bottom
A message was encrypted with three different 1,024-bit RSA public keys (N_1, N_2, and N_3), resulting
in three different ciphers (c_1, c_2, and c_3). All of them have the same public exponent ???? = 3.
You are given the three pairs of public keys and associated ciphers. Your job is to write the code to
recover the original message.
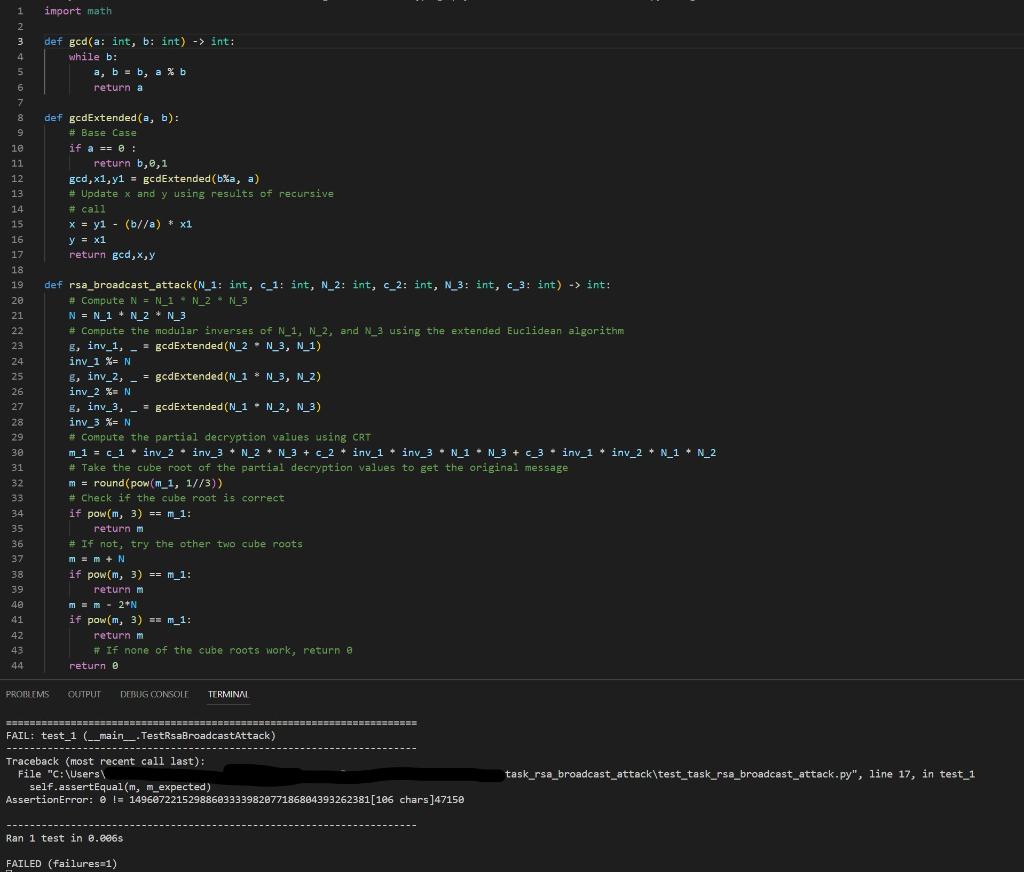
ATTEMPT 1 - SEE ERROR
import math
def rsa_broadcast_attack(N_1: int, c_1: int, N_2: int, c_2: int, N_3: int, c_3: int) -> int:
# Compute N = N_1 * N_2 * N_3
N = N_1 * N_2 * N_3
# Compute the modular inverses of N_1, N_2, and N_3
inv_1 = pow(N_1, -1, N) - ValueError: base is not invertible for the given modulus
inv_2 = pow(N_2, -1, N) - ValueError: base is not invertible for the given modulus
inv_3 = pow(N_3, -1, N) - ValueError: base is not invertible for the given modulus
# Compute the partial decryption values using CRT
m_1 = c_1 * inv_2 * inv_3 * N_2 * N_3 + c_2 * inv_1 * inv_3 * N_1 * N_3 + c_3 * inv_1 * inv_2 * N_1 * N_2
# Take the cube root of the partial decryption values to get the original message
m = round(pow(m_1, 1/3))
if pow(m, 3) == m_1:
return m
return 0
ATTEMPT 2 - TAKES TOO LONG
import math
def is_prime(n: int) -> bool:
if n <= 1:
return False
if n <= 3:
return True
if n % 2 == 0 or n % 3 == 0:
return False
i = 5
while i * i <= n:
if n % i == 0 or n % (i + 2) == 0:
return False
i += 6
return True
def rsa_broadcast_attack(N_1: int, c_1: int, N_2: int, c_2: int, N_3: int, c_3: int) -> int:
# Check if the keys are prime
if not is_prime(N_1) or not is_prime(N_2) or not is_prime(N_3):
return 0
# Compute N = N_1 * N_2 * N_3
N = N_1 * N_2 * N_3
# Compute the modular inverses of N_1, N_2, and N_3
inv_1 = pow(N_1, -1, N)
inv_2 = pow(N_2, -1, N)
inv_3 = pow(N_3, -1, N)
# Compute the partial decryption values using CRT
m_1 = c_1 * inv_2 * inv_3 * N_2 * N_3 + c_2 * inv_1 * inv_3 * N_1 * N_3 + c_3 * inv_1 * inv_2 * N_1 * N_2
m_2 = m_1 - N
m_3 = m_1 + N
# Take the cube root of the partial decryption values to get the original message
m = round(pow(m_1, 1/3))
if pow(m, 3) == m_1:
return m
m = round(pow(m_2, 1/3))
if pow(m, 3) == m_2:
return m
m = round(pow(m_3, 1/3))
if pow(m, 3) == m_3:
return m
return 0
ATTEMPT 3 - SIMPLY FAILING:
import math
import random
def gcd(a: int, b: int) -> int:
while b:
a, b = b, a % b
return a
def is_prime(n: int, k: int = 10) -> bool:
if n <= 1:
return False
if n in (2, 3):
return True
if n % 2 == 0:
return False
# Write n-1 as 2^r*d where d is odd
r, d = 0, n - 1
while d % 2 == 0:
r += 1
d //= 2
# Test for k rounds
for _ in range(k):
a = random.randint(2, n - 2)
x = pow(a, d, n)
if x == 1 or x == n - 1:
continue
for _ in range(r - 1):
x = pow(x, 2, n)
if x == n - 1:
break
else:
return False
return True
def rsa_broadcast_attack(N_1: int, c_1: int, N_2: int, c_2: int, N_3: int, c_3: int) -> int:
# Check if the keys are prime
if not is_prime(N_1) or not is_prime(N_2) or not is_prime(N_3):
return 0
# Compute N = N_1 * N_2 * N_3
N = N_1 * N_2 * N_3
# Compute the modular inverses of N_1, N_2, and N_3
inv_1 = pow(N_1, -1, N)
inv_2 = pow(N_2, -1, N)
inv_3 = pow(N_3, -1, N)
# Compute the partial decryption values using CRT
m_1 = c_1 * inv_2 * inv_3 * N_2 * N_3 + c_2 * inv_1 * inv_3 * N_1 * N_3 + c_3 * inv_1 * inv_2 * N_1 * N_2
# Take the cube root of the partial decryption values to get the original message
m = round(pow(m_1, 1//3))
if pow(m, 3) == m_1:
return m
m = round(pow(m_1 - N, 1//3))
if pow(m, 3) == m_1:
return m
m = round(pow(m_1 + N, 1//3))
if pow(m, 3) == m_1:
return m
return 0
Traceback (most recent call last):
File "C:\Users\*\task_rsa_broadcast_attack\test_task_rsa_broadcast_attack.py", line 17, in test_1
self.assertEqual(m, m_expected)
AssertionError: 0 != 14960722152988603333982077186804393262381[106 chars]47150
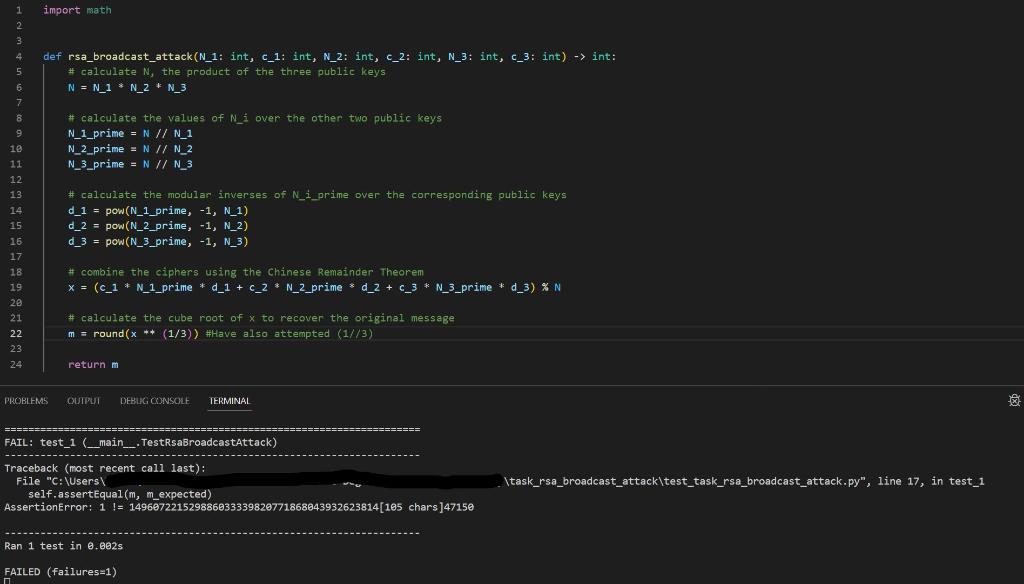
ATTEMPT 4 - SIMPLY FAILING
ATTEMPT 5
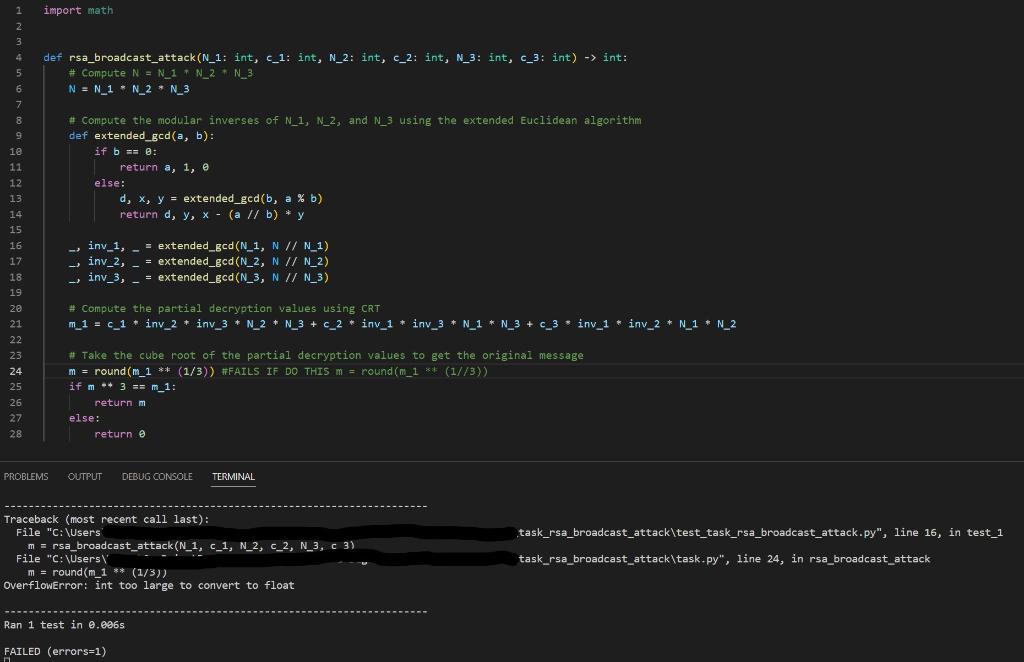
ATTEMPT 6 - INT TOO LARGE TO CONVER TO FLOAT
ATTEMPT 7 - CODE EXACT SAME AS 5
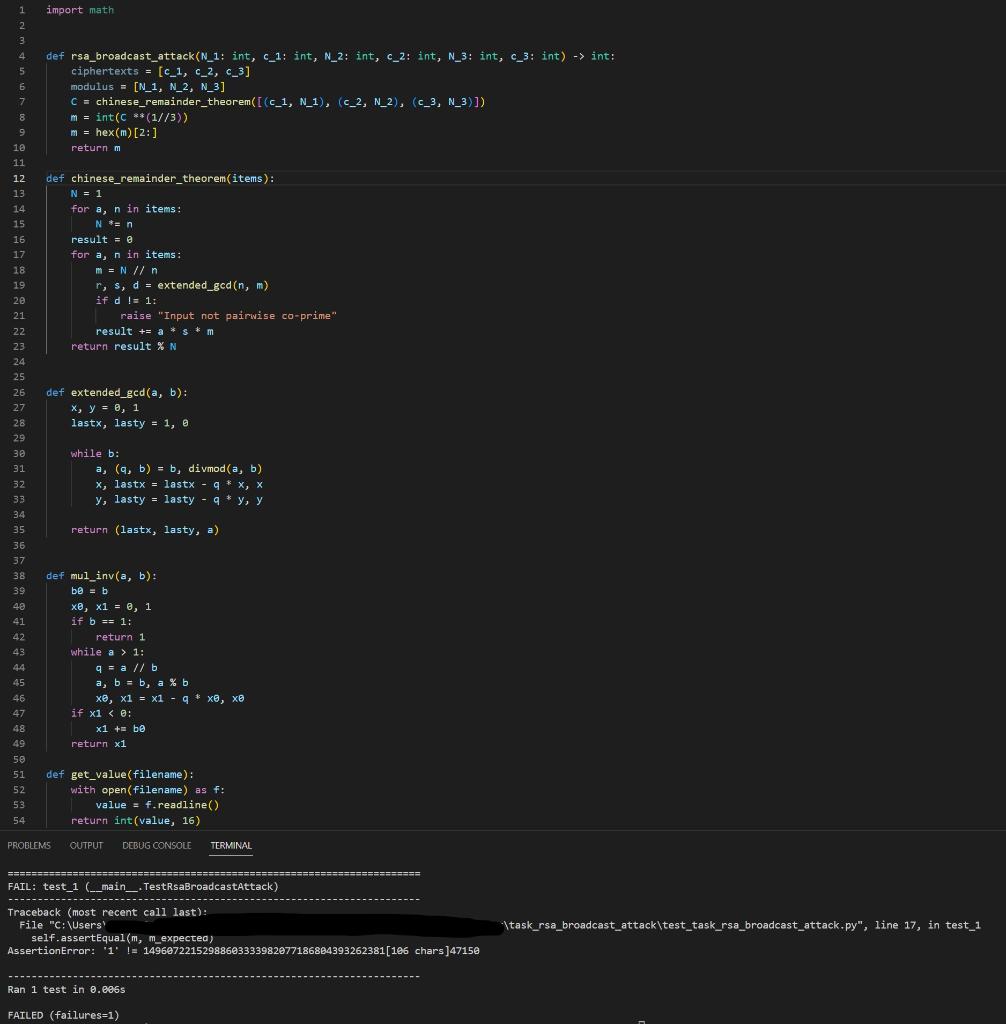
ATTEMPT 8 - Appears to be missing 106 characters
I'm not seeing where I am missing it.
ATTEMPT 9 ANSWER I RECIEVED WITH CODE - NEEDS TO BE ABLE TO WORK WITH LARGE NUMBERS
The changes made in the above code are:
Added a function gcd to compute the greatest common divisor of two numbers.
Modified the rsa_broadcast_attack function to check if N_1, N_2, and N_3 are coprime. If they are not, then there is no unique solution to the RSA Broadcast Attack, and the function should return 0.
Removed the is_prime function as it is not needed.
Corrected the computation of the modular inverses of N_1, N_2, and N_3.
Corrected the computation of the partial decryption values using CRT by adding parentheses to ensure that the modular arithmetic is performed correctly.
Removed the unused import math.