(Solved): Solve both equations Let's model this situation with a 2nd order ODE. Recall that the governing e ...

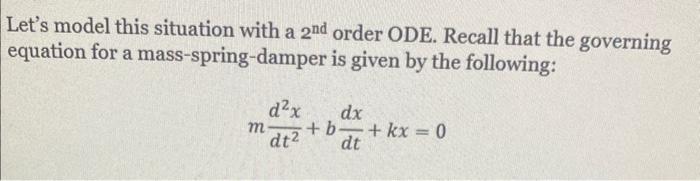
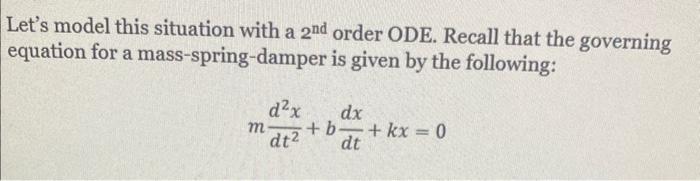
Let's model this situation with a $$2^{\text{nd }}$$ order ODE. Recall that the governing equation for a mass-spring-damper is given by the following: $$m\frac{d^{2}x}{d{t}^2}+b\frac{dx}{dt}+kx=0$$ Where $$m$$ is the mass of the tire, $$b$$ is the damping constant, and $$k$$ is the spring constant. Let's assume these values for $$m=15,k=2564$$, and $$b=$$ 144. We wish to perform a bounce test to see if our shock absorbers are still in good condition. Answer the following questions: a. Solve for the general solution of the differential equation. Use your calculator to compute the roots in decimals instead of the fractions. - Ans: $$x(t)=e^{?4.8t}[A\cos (12.16t)+B\sin (12.16t)]$$ b. We can model a bounce test by setting the initial displacement equal to 20 (i.e. $$x(0)=20$$ ). Assume that the system starts from rest (i.e. $$x^{?}(0)=0$$ ). Solve the initial value problem. - Ans: $$x(t)=e^{?4.8t}[20\cos (12.16t)+7.89\sin (12.16t)]$$