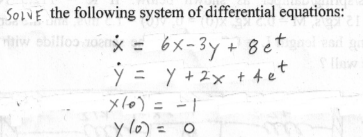Home /
Expert Answers /
Mechanical Engineering /
solve-the-following-system-of-differential-equations-x-6x3y-8ety-y-2x-4etx-0-1y-0-pa187
Expert Answer
(A): Given the differential equations:x' = 6x - 3y + 8ety' = y + 2x + 4etThe given conditions are:x(0) = -1y(0) = 0To solve the system, we can use the method of integrating factors. Then, the integrating factor for the first equation is given by: note that the differentiation had done to the above equation. Multiply both sides of the first equation by :that means we have to substitute the equation in the first (x') differential equation.e6tx' = 6e6tx - 3e6ty + 8et*e6te6tx' = 6e6tx - 3e6ty + 8e7t