(Solved): Suppose a simple random. sample of size \( \mathrm{n}=1000 \) is obtained from a population whose s ...

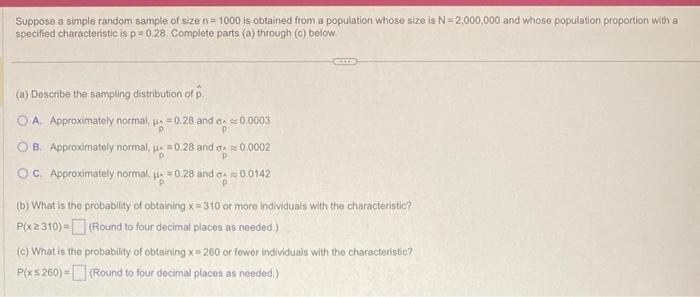
Suppose a simple random. sample of size \( \mathrm{n}=1000 \) is obtained from a population whose size is \( \mathrm{N}=2,000,000 \) and whose population proportion with a specified characteristic is \( p=0.28 \). Complete parts (a) through (c) below. (a) Describe the sampling distribution of \( \hat{\mathrm{p}} \). A. Approximately notmal, \( \mu_{\hat{p}}=0.28 \) and \( \sigma_{\hat{p}} \approx 0.0003 \) B. Approximately normal, \( \mu_{p}=0.28 \) and \( \sigma_{p} \approx 0.0002 \) C. Approximately normal, \( \mu_{p}=0.28 \) and \( \sigma_{p}, \approx 0.0142 \) (b) What is the probability of obtaining \( x=310 \) or more individuals with the characteristic? \( P(x \geq 310)=\quad \) (Round to four decimal places as needed.) (c) What is the probability of obtaining \( x=260 \) or fewer individuals with the characteristic? \( P(x \leq 260)=\quad \) (Round to four decimal places as needed.)