(Solved): Suppose F(x,y)=2y,sin(y) and C is the circle of radius 6&nbs ...

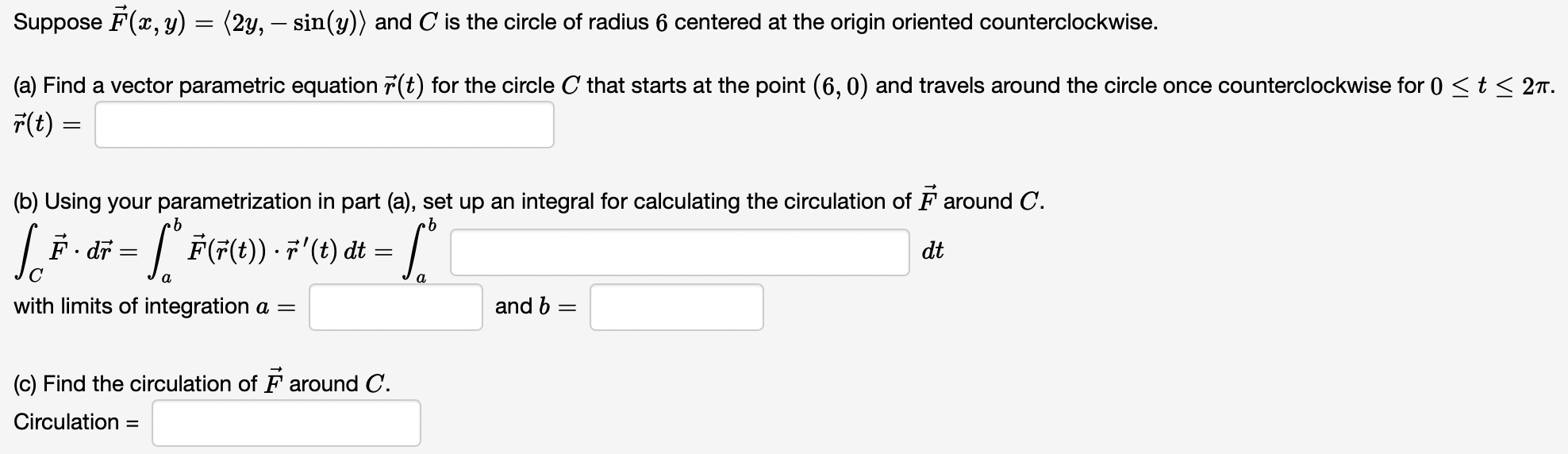
Suppose F?(x,y)=?2y,?sin?(y)? and C is the circle of radius 6 centered at the origin oriented counterclockwise. 

(a) Find a vector parametric equation r?(t) for the circle C that starts at the point (6,0) and travels around the circle once counterclockwise for 0?t?2?.  
r?(t)=  

(b) Using your parametrization in part (a), set up an integral for calculating the circulation of F? around C. 
?CF??dr?=?abF?(r?(t))?r??(t)dt=?ab  dt 
with limits of integration a=  and b=  

(c) Find the circulation of F? around C. 
Circulation = 

Suppose \( \vec{F}(x, y)=\langle 2 y,-\sin (y)\rangle \) and \( C \) is the circle of radius 6 centered at the origin oriented counterclockwise. (a) Find a vector parametric equation \( \vec{r}(t) \) for the circle \( C \) that starts at the point \( (6,0) \) and travels around the circle once counterclockwise for \( 0 \leq t \leq 2 \pi \). \( \vec{r}(t)= \) (b) Using your parametrization in part (a), set up an integral for calculating the circulation of \( \vec{F} \) around \( C \). \[ \int_{C} \vec{F} \cdot d \vec{r}=\int_{a}^{b} \vec{F}(\vec{r}(t)) \cdot \vec{r}^{\prime}(t) d t=\int_{a}^{b} \] with limits of integration \( a=\quad \) and \( b= \) (c) Find the circulation of \( \vec{F} \) around \( C \).