Home /
Expert Answers /
Electrical Engineering /
the-answer-is-shown-below-please-show-all-the-missing-work-using-the-same-method-solve-t-pa600
(Solved): The answer is shown below please show all the missing work using the same method. Solve t ...
The answer is shown below please show all the missing work using the same method.
Solve the following equations using both the direct method and the convolution method. (a) \( \left(D^{2}+7 D+12\right) y(t)=e^{t} \xi(t), \quad y(0)=\left.\frac{d y(t)}{d t}\right|_{t=0}=0 \) (b) \( \left(D^{2}+3 D+2\right) y(t)=e^{-t} \xi(t), \quad y(0)=\left.\frac{d y(t)}{d t}\right|_{t=0}=0 \)
a) \[ \begin{array}{l} \left(D^{2}+7 D+12\right) y(t)=e^{t} \zeta(t) \\ y(0)=\left.\frac{d y(t)}{d t}\right|_{t=0}=0 \\ L_{A}=D-1 \\ (D-1)\left(D^{2}+7 D+12\right) y(t)=0 \\ (r-1)\left(r^{2}+7 r+12\right)=0 \rightarrow r_{1}=-3, r_{2}=-4, r_{3}=1 \\ y(t)=c_{1} e^{t}+c_{2} e^{-4 t}+c_{3} e^{-3 t} \\ \left(D^{2}+7 D+12\right) y(t)=20 c_{1} e^{t}=e^{t} \rightarrow c_{1}=\frac{1}{20} \\ y(0)=\frac{1}{20}+c_{2}+c_{3}=0 \end{array} \]
\[ \begin{array}{l} \left.\frac{d y(t)}{d t}\right|_{t=0}=\frac{1}{20}-4 c_{2}-3 c_{3}=0 \rightarrow\left\{\begin{array}{c} c_{2}=\frac{1}{5} \\ c_{3}=-\frac{1}{4} \end{array}\right. \\ y(t)=\frac{1}{20} e^{t}+\frac{1}{5} e^{-4 t}-\frac{1}{4} e^{-3 t} \end{array} \] By convolution, from \( 3.8 \) a, we have: \[ h(t)=\left(e^{-3 t}-e^{-4 t}\right) \zeta(t) \] Thus: \[ \begin{aligned} y(t) &=\int_{0}^{t}\left(e^{-3 \tau}-e^{-4 \tau}\right) e^{t-\tau} d \tau \\ &=e^{t} \frac{e^{-4 t}-1}{-4}-e^{t} \frac{e^{-5 t}-1}{-5} \\ &=\frac{1}{20} e^{t}-\frac{1}{4} e^{-3 t}+\frac{1}{5} e^{-4 t}, t \geq 0 \end{aligned} \]
b) The first part is identical to problem \( 3.6 \) (b), from which \[ y(t)=(t-1) e^{-t}+e^{-2 t}, t \geq 0 \] By convolution, we have: \[ \begin{array}{l} \left(r^{2}+3 r+2\right)=0 \rightarrow r_{1}=-1, r_{2}=-2 \\ h(t)=c_{1} e^{-t}+c_{2} e^{-2 t} \\ h(0)=c_{1}+c_{2}=0 \\ \left.\frac{d h(t)}{d t}\right|_{t=0}=-c_{1}-2 c_{2}=1 \rightarrow\left\{\begin{array}{c} c_{1}=1 \\ c_{2}=-1 \end{array}\right. \\ h(t)=\left(e^{-t}-e^{-2 t}\right) \zeta(t) \end{array} \] Thus: \[ \begin{aligned} y(t) &=h(t) * u(t) \\ &=\int_{0}^{t}\left(e^{-\tau}-e^{-2 \tau}\right) e^{-(t-\tau)} d \tau \\ &=e^{-t}\left\{\int_{0}^{t} 1 d \tau-\int_{0}^{t} e^{-\tau} d \tau\right\} \\ &=e^{-t}\left\{t-\frac{e^{-t}-1}{-1}\right\} \end{aligned} \]
\( =t e^{-t}-e^{-t}+e^{-2 t}, t \geq 0 \)


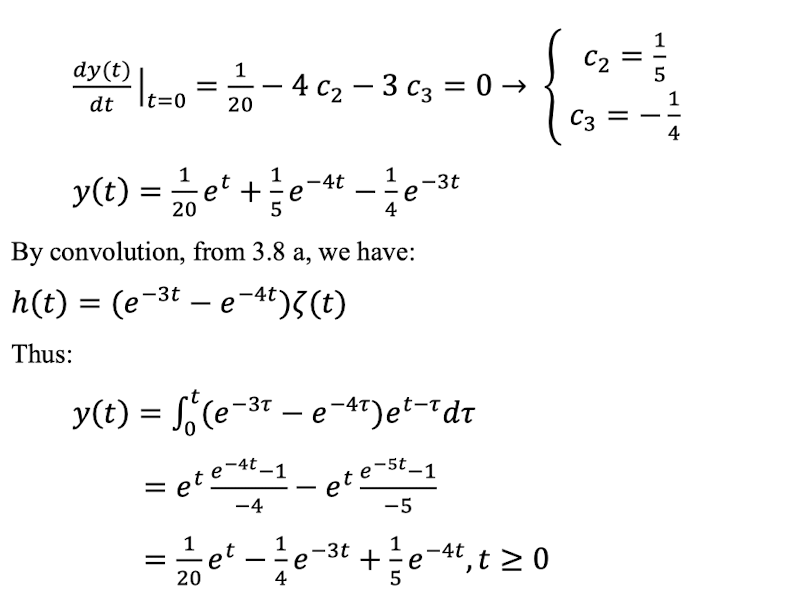
![b)
The first part is identical to problem \( 3.6 \) (b), from which
\[
y(t)=(t-1) e^{-t}+e^{-2 t}, t \geq 0
\]
By convolution](https://media.cheggcdn.com/media/fbe/fbed8901-1434-4357-98de-3f863057c2c6/phpQg0368)
