Home /
Expert Answers /
Advanced Math /
the-cotb-douglas-producton-function-for-a-partedar-poctuct-is-n-x-y-40x00-6y0-4-where-x-in-the-pa838
(Solved): The Cotb Douglas producton function for a partedar poctuct is N(x,y)=40x00.6y0.4, where x in the ...
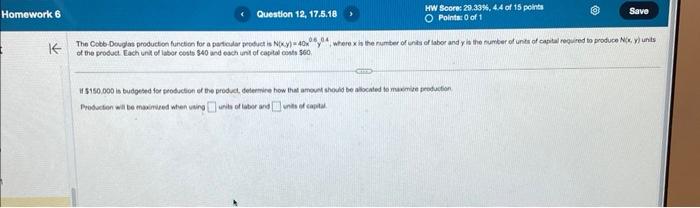
The Cotb Douglas producton function for a partedar poctuct is , where in the rumter of inits of iabor and is the tumber of unis of captal regured bo produce Nak. ) unts of the product Each bnil of labor cost and each unt of capital costs 560 H 5150,000 is budosted for producfion ef be product, delermire how that amoud should be alocated to maxmize troduction Probucten will be madirired when vaing units of laber and unis ef capad.
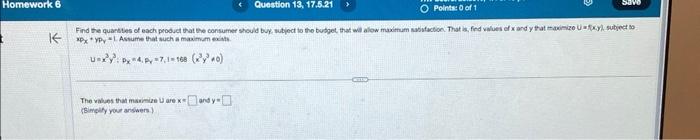
Find the quarbies of each product that ene consumer should buy, sutjpct to tho budget that wil alow maximum nabifacton. That is. find vilues of and y that maimizo U of (x.yl. subject so . Astume that such a masimum noith. The valuns that maximias 13 are and ;simelty your answers)
Expert Answer
To maximize production, we need to determine the optimal allocation of the budget between labor and capital. Let the number of units of labor be denoted by L and the number of units of capital be denoted by K. We have a budget of $515,000, which we can use to purchase labor and capital. The cost of one unit of labor is $40, and the cost of one unit of capital is $560. Therefore, we can write the budget constraint as: The production function is given by: where x is the number of units of labor and y is the number of units of capital required to produce N units of the product.To maximize production, we need to maximize the production function subject to the budget constraint. We can use the Lagrange multiplier method to solve this optimization problem.