Home /
Expert Answers /
Algebra /
the-eigenvectors-of-a-square-matrix-a-are-all-non-zero-vectors-v-such-that-av-lambda-v-for-some-pa660
(Solved): The eigenvectors of a square matrix A are all non-zero vectors v such that Av=\lambda v for some ...
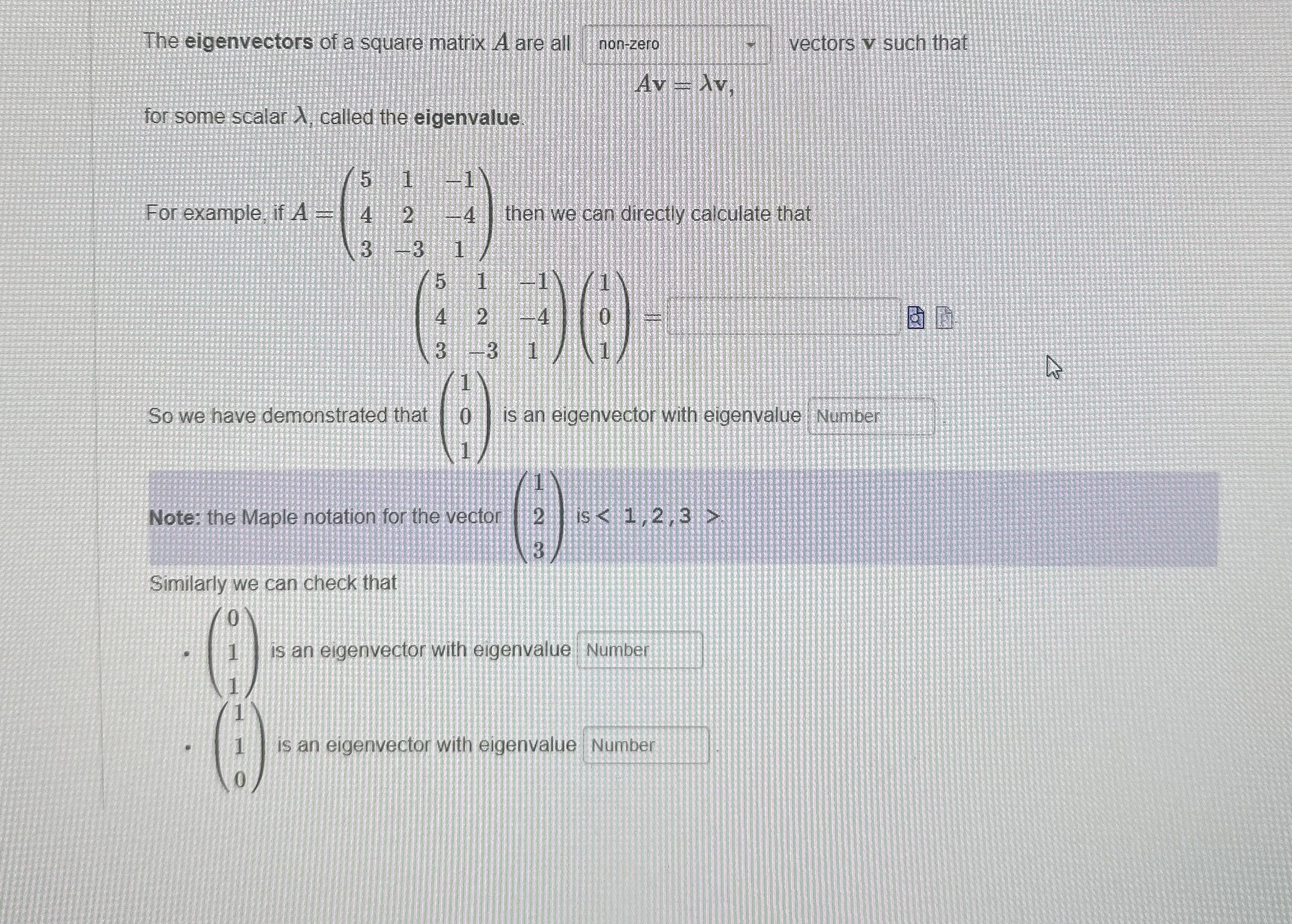
The eigenvectors of a square matrix
Aare all
◻non-zero vectors
vsuch that
Av=\lambda vfor some scalar
\lambda , called the eigenvalue For example if
A=([5,1,-1],[4,2,-4],[3,-3,1])then we can directly calculate that
([5,1,-1],[4,2,-4],[3,-3,1])([1],[0],[1])=
◻9.
([5,1,-1],[4,2,-4],[3,-3,1])([1],[0],[1])=a So we have demonstrated that
([1],[0],[1])is an eigenvector with eigenvalue Number Note: the Maple notation for the vector
([1],[2],[3])is
{(
:<1,2,3:)} Similarly we can check that
([0],[1],[1])is an eigenvector with eigenvalue
([1],[1],[0])is an eigenvector with eigenvalue
◻