Home /
Expert Answers /
Calculus /
the-ends-of-a-34-parabolic-34-water-tank-are-the-shape-of-the-region-inside-the-graph-of-y-x-2-for-pa607
(Solved): The ends of a "parabolic" water tank are the shape of the region inside the graph of y = x^(2) for ...
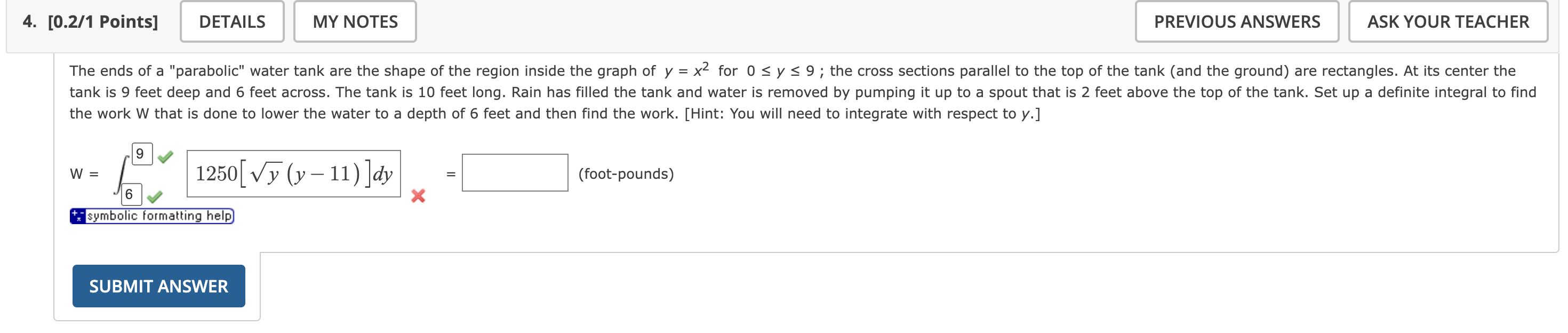
The ends of a "parabolic" water tank are the shape of the region inside the graph of
y = x^(2)
for
0 <= y <= 9
; the cross sections parallel to the top of the tank (and the ground) are rectangles. At its center the tank is 9 feet deep and 6 feet across. The tank is 10 feet long. Rain has filled the tank and water is removed by pumping it up to a spout that is 2 feet above the top of the tank. Set up a definite integral to find the work W that is done to lower the water to a depth of 6 feet and then find the work. [Hint: You will need to integrate with respect to y.]