(Solved): The estimated regression equation for these data is \( \hat{y}=21.993311+0.32 ...

???????

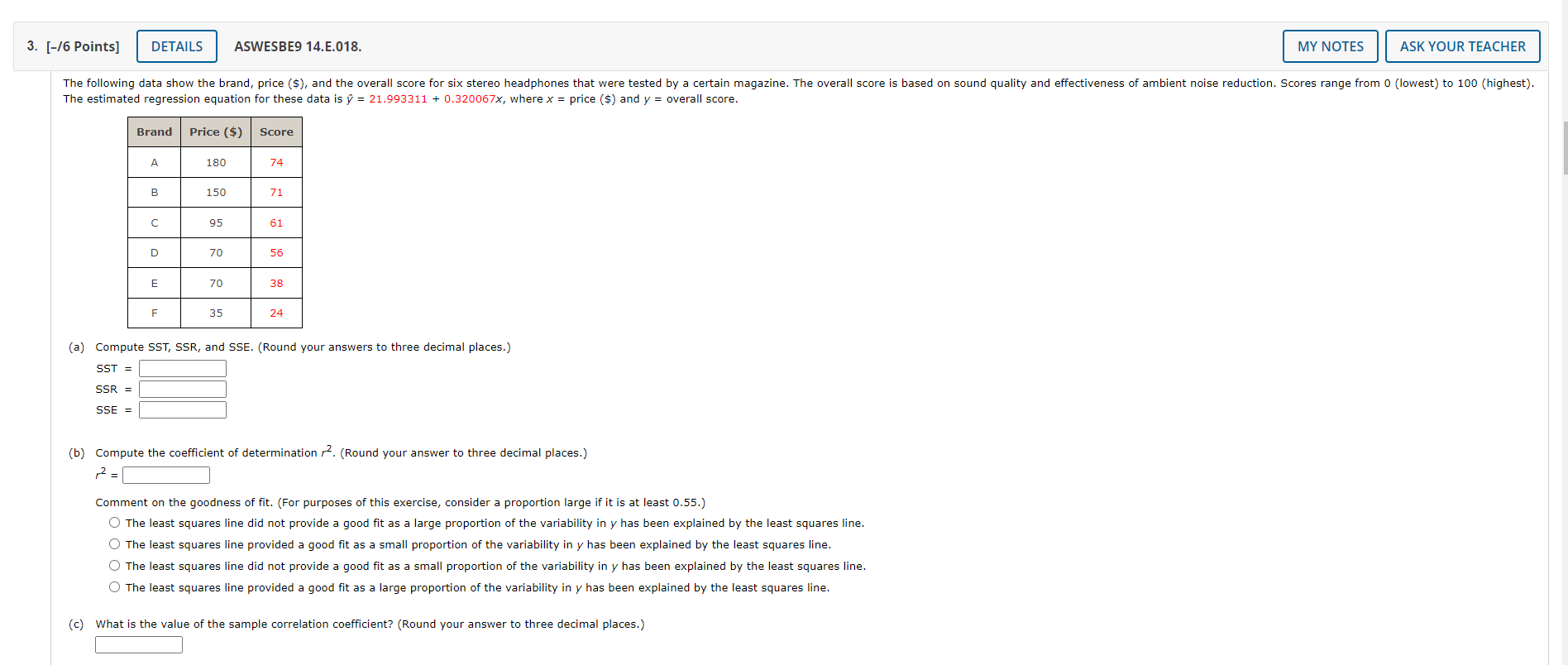
The estimated regression equation for these data is \( \hat{y}=21.993311+0.320067 x \), where \( x= \) price ( \( \$ \) ) and \( y= \) overall score. (a) Compute SST, SSR, and SSE. (Round your answers to three decimal places.) \[ \begin{array}{l} \mathrm{SST}= \\ \mathrm{SSR}= \\ \mathrm{SSE}= \end{array} \] (b) Compute the coefficient of determination \( r^{2} \). (Round your answer to three decimal places.) \( r^{2}= \) Comment on the goodness of fit. (For purposes of this exercise, consider a proportion large if it is at least \( 0.55 \). .) The least squares line did not provide a good fit as a large proportion of the variability in \( y \) has been explained by the least squares line. The least squares line provided a good fit as a small proportion of the variability in \( y \) has been explained by the least squares line. The least squares line did not provide a good fit as a small proportion of the variability in \( y \) has been explained by the least squares line. The least squares line provided a good fit as a large proportion of the variability in \( y \) has been explained by the least squares line. (c) What is the value of the sample correlation coefficient? (Round your answer to three decimal places.)