Home /
Expert Answers /
Advanced Math /
the-linear-transformation-t-r-6-gt-r-6-below-is-nilpotent-of-nilpotency-index-4-t-x-1-x-2-pa793
(Solved): The linear transformation T:R^(6)->R^(6) below is nilpotent of nilpotency index 4 . T(x_(1),x_(2) ...
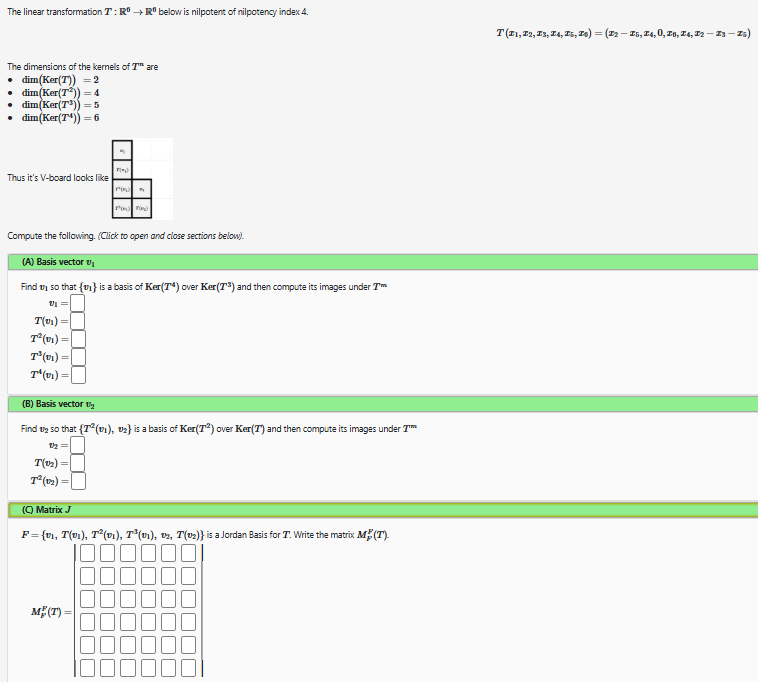
The linear transformation T:R^(6)->R^(6) below is nilpotent of nilpotency index 4 .
T(x_(1),x_(2),x_(3),x_(4),x_(5),x_(5))=(x_(2)-x_(5),x_(4),0,x_(6),x_(4),x_(2)-x_(3)-x_(5))
The dimensions of the kernels of T^(m) are
dim(Ker(T^(')))=2
dim(Ker(T^(2)))=4
dim(Ker(T^(3)))=5
dim(Ker(T^(4)))=6
Compute the following. (Click to open and close sections below).
(A) Basis vector v_(1)
Find v_(1) so that {v_(1)} is a basis of Ker(T^(4)) over Ker(T^(3)) and then compute its images under T^(m)
v_(1)=
T(v_(1))=
T^(2)(v_(1))=
T^(3)(v_(1))=
T^(4)(v_(1))=
(B) Basis vector v_(2)
Find v_(2) so that {T^(2)(v_(1)),v_(2)} is a basis of Ker(T^(2)) over Ker(T^(')) and then compute its images under T^(m)
v_(2)=
T(v_(2))=
T^(2)(v_(2))=
(C) Matrix J
M_(F)^(F)