(Solved): The rectangles in the graph below illustrate a left endpoint Riemann sum for \( f(x)-\frac{-x^{2}} ...

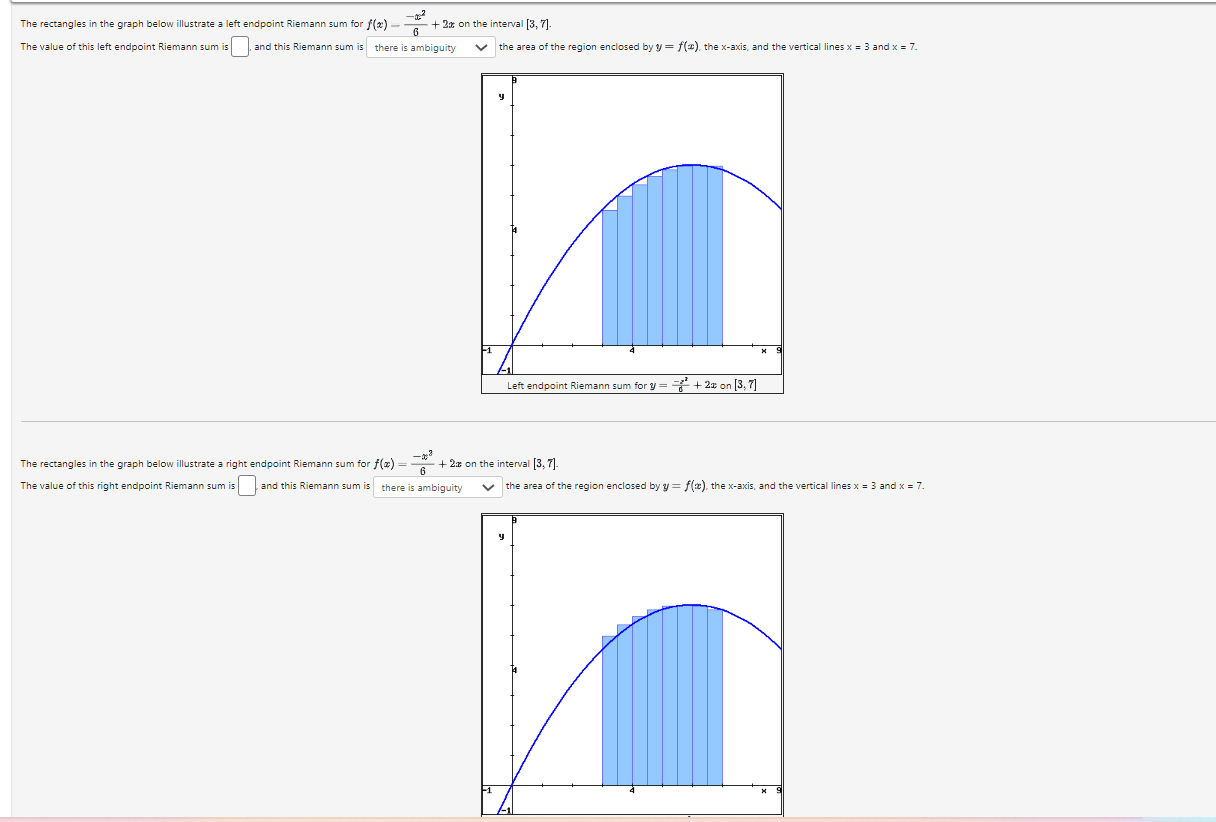
The rectangles in the graph below illustrate a left endpoint Riemann sum for \( f(x)-\frac{-x^{2}}{6}+2 x \) on the interval \( [3,7] \). The value of this left endpoint Riemann sum is and this Riemann sum is the area of the region enclosed by \( y=f(x) \), the \( x \)-axis, and the vertical lines \( x=3 \) and \( x=7 \). The rectangles in the graph below illustrate a right endpoint Riemann sum for \( f(x)=\frac{-x^{3}}{6}+2 x \) on the interval \( [3,7] \). The value of this right endpoint Riemann sum is and this Riemann sum is the area of the region enclosed by \( y=f(x) \), the \( x \)-axis, and the vertical lines \( x=3 \) and \( x=7 \).