(Solved): The samplio of six measurements shown below was randomly selected from a normally distributed popul ...

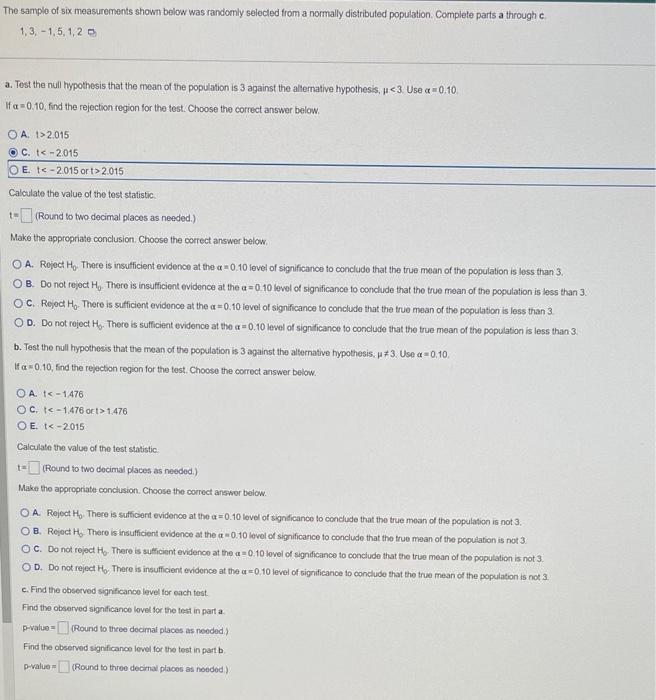
The samplio of six measurements shown below was randomly selected from a normally distributed population. Complete parts a through c. \[ 1,3,-1,5,1,2 \text { ? } \] a. Test the null hypothesis that the mean of the population is 3 against the allemative hypothesis, \( \mu<3 \) Use \( \alpha=0.10 \). If \( \alpha=0.10 \), find the rejection region for the test. Choose the correct answer below. A. \( 1>2.015 \) C. \( t<-2.015 \) E. \( t<-2.015 \) or \( t>2.015 \) Calculate the value of the test statistic. t= (Round to two decimal places as needed.) Make the appropriate conclusion. Choose the correct answer below. A. Roject \( \mathrm{H}_{0} \). Thece is insulficient evidence at the \( \alpha=0.10 \) level of significance to conclude that the true mean of the population is less than 3 . B. Do not reject \( \mathrm{H}_{0} \). There is insufficient evidence at the \( \alpha=0.10 \) level of significance to condude that the true mean of the population is less than 3 . C. Rcject \( \mathrm{H}_{0} \). There is sufficient evidence at the \( \alpha=0 \). 10 level of significance to conclude that the true mean of the population is less than 3 . D. Do not reject \( H_{0} \). There is sufficient evidence at the \( \alpha=0.10 \) level of significance to condlude that the true mean of the population is less than 3 . b. Test the null hypothesis that the mean of the population is 3 against the alternative hypothesis; \( \mu \neq 3 \), Use \( \alpha=0.10 \). If \( \alpha=0.10 \), find the rejection region for the test. Choose the correct answer below. A. \( t<-1.476 \) C. \( t<-1.476 \) oc \( t>1.476 \) E. \( t<-2.015 \) Calculate the value of the test statistic. \( t= \) (Round to two decimal places as needed.) Make the appropriate conclusion. Choose the conect answer beiow. A. Rejoct \( \mathrm{H}_{0} \). There is sufficiert evidence at the \( \mathrm{\alpha}=0.10 \) level of significance to conclude that the true mean of the population is not 3 . B. Rejoct \( \mathrm{H}_{0} \). There is insufficient evidence at the \( \alpha=0.10 \) levol of sigrificance to conclude that the true mean of the population is not 3. c. Do not refect \( \mathrm{H}_{0} \). There is sueficient evidenco at the \( \alpha=0.10 \) lovel of significance to conclude that the true mean of the population is not 3. D. Do not rejed \( \mathrm{H}_{0} \). There is insufficient evidence at the \( \mathrm{\alpha}=0.10 \) level of significance to condude that the thwe mean of the population is not 3. c. Find the observed significance level for each test. Find the observed signticance lovel for the test in part a. p-value \( = \) (Round to three docimal places as nooded)