Home /
Expert Answers /
Advanced Math /
the-temperature-at-a-point-x-y-is-t-x-y-measured-in-degrees-celsius-a-bug-crawls-so-th-pa199
(Solved): The temperature at a point (x, y) is T(x, y), measured in degrees Celsius. A bug crawls so th ...
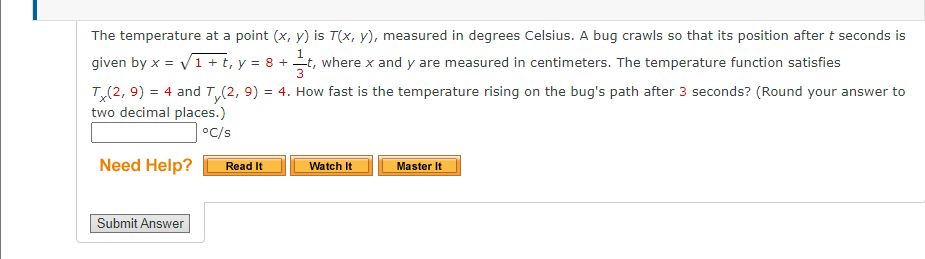
The temperature at a point (x, y) is T(x, y), measured in degrees Celsius. A bug crawls so that its position after t seconds is given by x = The temperature at a point
(x,y)is
T(x,y), measured in degrees Celsius. A bug crawls so that its position after
tseconds is given by
x=\sqrt(1+t),y=8+(1)/(3)t, where
xand
yare measured in centimeters. The temperature function satisfies
T_(x)(2,9)=4and
T_(y)(2,9)=4. How fast is the temperature rising on the bug's path after 3 seconds? (Round your answer to two decimal places.)
\deg (C)/(s)Need Help? 1 + t , y = 8 + 1 3 t, where x and y are measured in centimeters. The temperature function satisfies Tx(2, 9) = 4 and Ty(2, 9) = 4. How fast is the temperature rising on the bug's path after 3 seconds? (Round your answer to two decimal places.) \deg C/s