The total differential approximation works in three-dimensional space, too. For example, consider the paraboloid z=F(x,y)=(x^(2))/(2^(2))+(y^(2))/(5^(2)) at the point 1,5,(5)/(4). The total differential approximation to z=F(x,y) near 1,5 is given by the formula F(x,y)~~(5)/(4)+(delF)/(delx)(1,5)(x-1)+(delF)/(dely)(1,5)(y-5) In fact, this gives the

Question

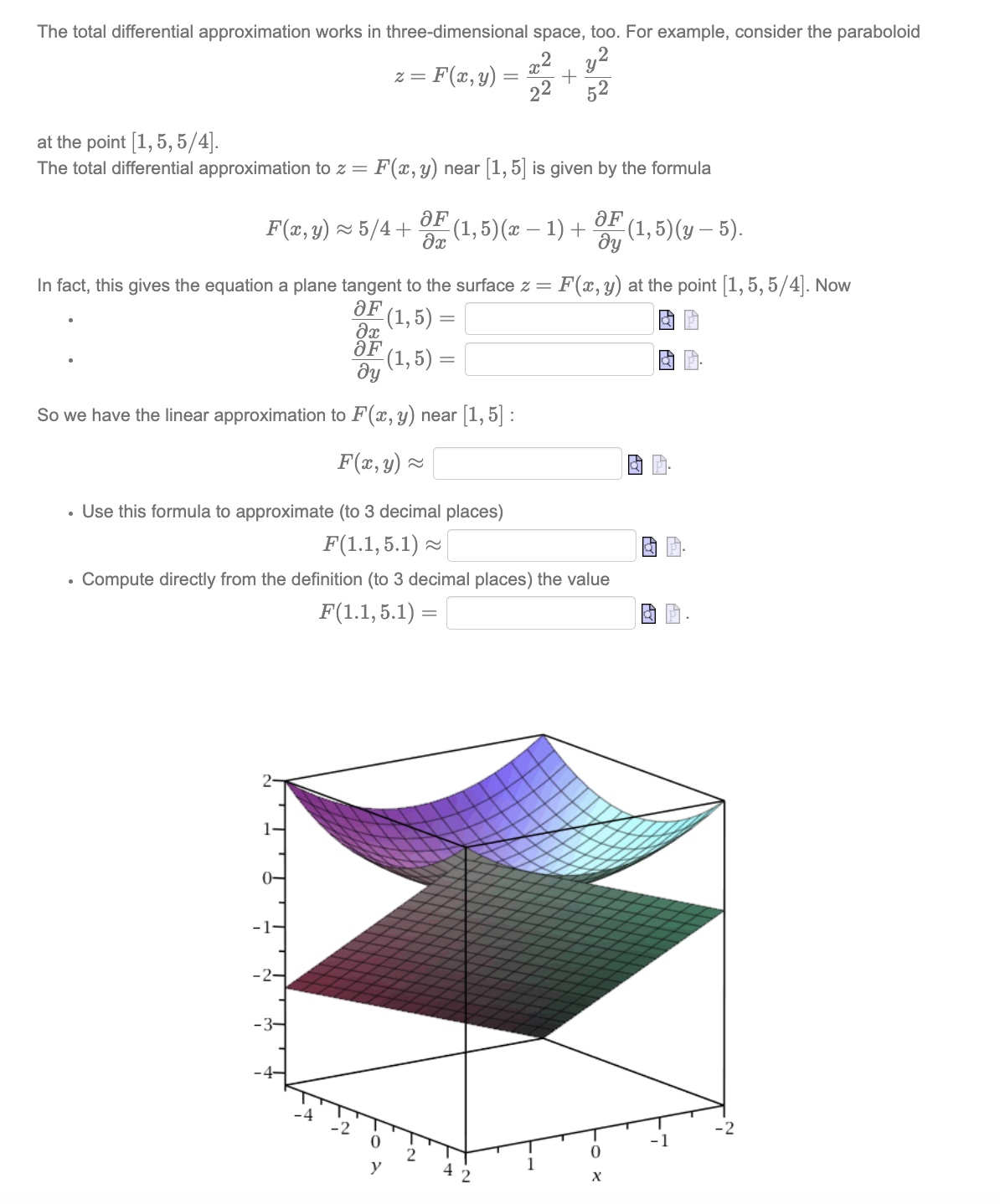
The total differential approximation works in three-dimensional space, too. For example, consider the paraboloid

z=F(x,y)=(x^(2))/(2^(2))+(y^(2))/(5^(2))

at the point

1,5,(5)/(4)

. The total differential approximation to

z=F(x,y)

near

1,5

is given by the formula

F(x,y)~~(5)/(4)+(delF)/(delx)(1,5)(x-1)+(delF)/(dely)(1,5)(y-5)

In fact, this gives the equation a plane tangent to the surface

z=F(x,y)

at the point

1,5,(5)/(4)

. Now

(delF)/(delx)(1,5)=
(delF)/(dely)(1,5)=

Q 줨. So we have the linear approximation to

F(x,y)

near

1,5

:

F(x,y)~~

Use this formula to approximate (to 3 decimal places)

F(1.1,5.1)~~

囯 Compute directly from the definition (to 3 decimal places) the value

F(1.1,5.1)=

图

Accepted Answer

Expert Answer to -  The total differential approximation works in three-dimensional space, too. For example, consider t

Answer

Solution for -  The total differential approximation works in three-dimensional space, too. For example, consider t

Answer

This an additional answer to -  The total differential approximation works in three-dimensional space, too. For example, consider t

(Solved): The total differential approximation works in three-dimensional space, too. For example, consider t ...