(Solved): the transfert function is attached. he was close to find the answers but apparently did something wr ...

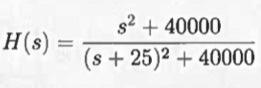
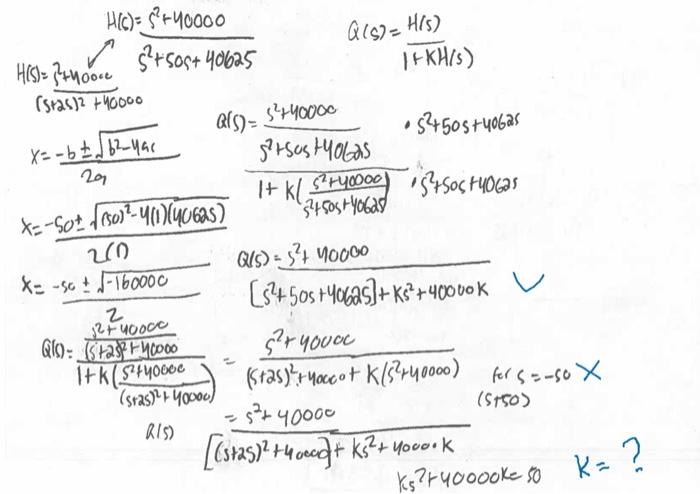
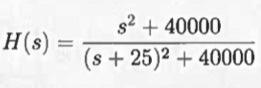
$H(s)=\frac{s^2+40000}{(s+25{)}^2+40000}$ (b) (15\%) The circuit in (a) has poles that are too close to the imaginary axis. Proportional feedback control $(G(s)=K)$ is used to move the poles farther to the left in the $s$ plane. The closed-loop poles must have a real part equal to -50 . Find the appropriate values for the coefficient $K$. (Note: the imaginary part of the poles may change too, and this is acceptable.) Proportional (P) Feedback: we choose $G(s)=K$ $\square$ For systems with a single pole, it is sufficient afor systems with $\ge 2$ poles, it may be insufficient $\square$ We need more flexibility (degrees of freedom) Control Theory Proportional +Derivative (PD) Feedback: $G(s)=K_1+K_{2}s$ Proportional +Integral (PI) Feedback: $G(s)=K_1+\frac{K_2}{s}$ Prop. + Integral +Derivative (PID) Feedback: $G(s)=K_1+K_{2}s+\frac{K_3}{s}$ $\begin{array}{l}(s+2s{)}^2+40000\\ \begin{array}{l}x=\frac{-b\pm \sqrt{b^2-4ac}}{2a}a(s)=\frac{s^2+40000}{s^2+50s+4062s}\cdot s^2+50s+406as\\ x=\frac{-50\pm \sqrt{(s0{)}^2-4(1)(40625)}}{2(0)}\end{array}\\ x=\frac{-sc\pm \sqrt{-160000}}{s^2+40000}Q(s)=\frac{s^2+40000}{\left[s^2+50s+40625\right]+k{s}^2+40000k}\\ Q(s)=\frac{\frac{s^2+40000}{(s+2s{)}^2+40000}}{1+k\left(\frac{s+40000}{(s+2s{)}^2+40000}\right)}=\frac{s^2+40000}{(s+2s{)}^2+40000+k\left(s^2+40000\right)}\begin{array}{l}\text{ for }s=-50X\\ (s+50)\end{array}\end{array}$