(Solved): This question has 2 parts. Part 1: The drawing below shows a Hasse diagram for a partial order o ...

This question has 2 parts. Part 1: The drawing below shows a Hasse diagram for a partial order on the set: \[ \{A, B, C, D, E, F, G, H, I, J\} \] Figure 1: A Hasse diagram shows 10 vertices and 8 edges. The vertices, represented by dots, are as follows: vertex \( J \) is upward of vertex \( H \); vertex \( H \) is upward of vertex \( I \); vertex \( B \) is inclined upward to the left of vertex \( A \); vertex \( C \) is upward of vertex \( B \); vertex \( D \) is inclined upward to the right of vertex \( C \); vertex \( E \) is inclined upward to the left of vertex \( F \); vertex \( G \) is inclined upward to the right of vertex E. The edges, represented by line segments between the vertices are as follows: 3 vertical edges connect the following vertices: \( B \) and \( C, H \) and \( I \), and \( H \) and \( J ; 5 \) inclined edges connect the following vertices: \( A \) and \( B, C \) and \( D, D \) and \( E, E \) and \( F \), and \( E \) and \( G \). Determine the properties of the Hasse diagram based on the following questions: (a) What are the minimal elements of the partial order? (b) What are the maximal elements of the partial order? (c) Which of the following pairs are comparable? 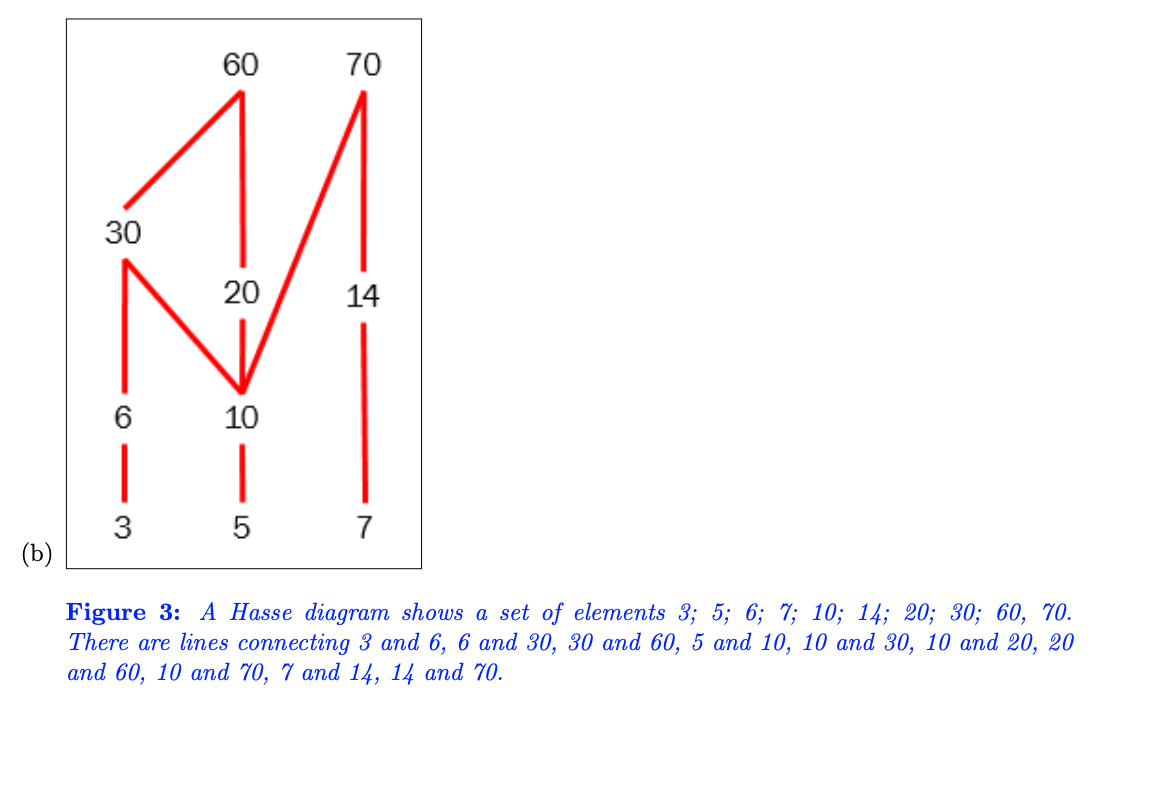\[ (A, D),(J, F),(B, E),(G, F),(D, B),(C, F),(H, I),(C, E) \] Part 2: Consider the partial order with domain \( \{3,5,6,7,10,14,20,30,60,70\} \) and with \( x \leq y \) if \( x \) evenly divides \( y \). Select the correct Hasse diagram for the partial order. (a) Figure 2: A Hasse diagram shows a set of elements 3; \( 5 ; 6 ; 7 ; 10 ; 14 ; 20 ; 30 ; 60,70 \). There are lines connecting 3 and 6, 6 and 30,30 and 60, 5 and 10,10 and 20,20 and 60,10 and 70,7 and 14, 14 and 70 . Figure 3: A Hasse diagram shows a set of elements \( 3 ; 5 ; 6 ; 7 ; 10 ; 14 ; 20 ; 30 ; 60,70 \). There are lines connecting 3 and 6, 6 and 30,30 and 60, 5 and 10,10 and 30,10 and 20, 20 and 60,10 and 70,7 and 14,14 and 70.