(Solved): trying to figure this error: Error using horzcat Dimensions of arrays being concatenated are not co ...

trying to figure this error:

Error using horzcat
Dimensions of arrays being concatenated are not consistent.

$\%$ Constants mu0 $=4^{\star }\mathrm{pi}{}^{\star }10^{\wedge }-7;$ ㅇacuum permeability \% Geometry and dimensions t0 $=0.02;$ Thickness of Omegal $\mathrm{b}0=0.02;\%$ Width of Omegal $ts=0.01;÷$ Thickness of Omega2 $g=0.001;÷$ Air-gap thickness $\mathrm{cD}=0.05;$ Distance from Omega2 to Gamma2 $10=0.05;÷$ Length of the domain $\mathrm{c}0=0.05;$ Distance from Omegal to Gammal \% Material properties mu1 $=1000;$ o Relative permeability of Omegal mu2 $=1;\%$ Relative permeability of Omega 2 $\%$ Boundary conditions $\mathrm{A}1=0;$ o Magnetic vector potential at Gammal A2 $=1e-3\star \mathrm{mu};$ 응 Magnetic vector potential at Gamma2 $\%$ Mesh generation $\mathrm{nx}=50;$ Number of elements along $x$-axis $\mathrm{ny}=50;$ Number of elements along $y$-axis $\mathrm{hx}=10/\mathrm{nx};$ Element size along $\mathrm{x}$-axis $\mathrm{hy}=\left(\mathrm{b}0+2{}^{\star }g\right)/$ ny; $\%$ Element size along $y$-axis \% Node and element numbering nodeNum $=(i,j)(j-1)\star (n\mathrm{n}+1)+i;$ elemNum $=(i,j)(j-1{)}^{\star }nx+i$ i \% Create nodes and elements nodes $=\mathrm{zeros}((nx+1)\star (ny+1),2)$; elements $=\mathrm{zeros}\left(n{x}^{\star }ny,4\right)$; for $j=1:ny+1$ for $i=1:nx+1$ nodes $(\mathrm{nodeNum}(i,j),:)=[(i-1)\star hx,(j-1)\star hy];$ end -end for $j=1:ny$ for $i=1:nx$ elements (elemNum $(i,j),:)=[\mathrm{nodeNum}(i,j),\mathrm{nodeNum}(i+1,j),\mathrm{nodeNum}(i+1,j+1),\mathrm{nodeNum}(i,j+1)]\mathbf{i}$ end -end \% Assemble global stiffness matrix and load vector numNodes $=(nx+1)\star (ny+1);$ 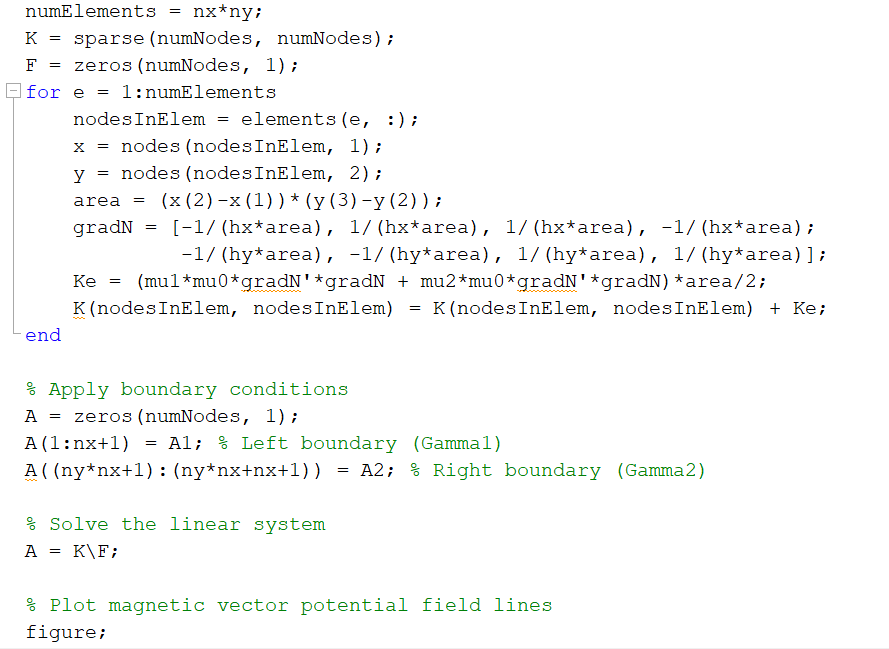numElements $=n{x}^{\star }ny;$ $\mathrm{K}=$ sparse (numNodes, numNodes); $\mathrm{F}=\mathrm{zeros}$ (numNodes, 1); for $e=1$ :numElements nodesInElem = elements $(e,:)$; $x=$ nodes (nodesInElem, 1 ); $y=$ nodes (nodesInElem, 2); area $=(x(2)-x(1))$ * $(y(3)-y(2))$; $\mathrm{Ke}=\left(\mathrm{mu}{1}^{\star }\mathrm{mu}{0}^{\star }{\mathrm{gradN}}^{\prime }{}^{\ast }\mathrm{gradN}+\mathrm{mu}{2}^{\star }\mathrm{mu}{0}^{\ast }\mathrm{gradN}{}^{\prime \ast }\mathrm{gradN}\right)$ *area $/2$; $\mathrm{K}$ (nodesInElem, nodesInElem) $=\mathrm{K}$ (nodesInElem, nodesInElem) $+\mathrm{Ke}$; end \% Apply boundary conditions $A=\mathrm{zeros}$ (numNodes, 1); $A(1:nx+1)=A1;÷$ Left boundary (Gamma1) $A\left(\left(n{y}^{\star }nx+1\right):\left(n{y}^{\star }nx+nx+1\right)\right)=A2;÷$ Right boundary (Gamma2) ° Solve the linear system $\mathrm{A}=\mathrm{K}\backslash \mathrm{F}$; \% Plot magnetic vector potential field lines figure; contourf(reshape(nodes $(:,1)$, ny+1, $nx+1)$, reshape(nodes $(:,2),ny+1,nx+1)$, reshape(A, ny+1, nx+1), 'LineColor', 'non hold on: quiver (reshape (nodes $(:,1)$, $ny+1,nx+1)$, reshape (nodes $(:,2),ny+1,nx+1)$, reshape (A, $ny+1$, $nx+1)$, zeros (ny+1, $nx+1)$, $\mathrm{xlabel}\left(\mathrm{xx}(\mathrm{m}{)}^{\prime }\right)$ $\mathrm{ylabel}\left(\mathrm{iy}(\mathrm{m}{)}^{\prime }\right)$ title('Magnetic Vector Potential Field Lines'); colorbar; axis equal; ° Compute total magnetic energy in the air-gap energy $=0$; for $e=1:$ numElements nodesInElem = elements $(e,:)$; $\mathrm{x}=\mathrm{nodes}($ nodesInElem, 1 ); $y=$ nodes (nodesInElem, 2); area $=(x(2)-x(1))\ast (y(3)-y(2))$; energy = energy + Ae; end