(Solved): TV sets: According to the Nielsen Company, the mean number of TV sets in a U.S. household was \( 2. ...

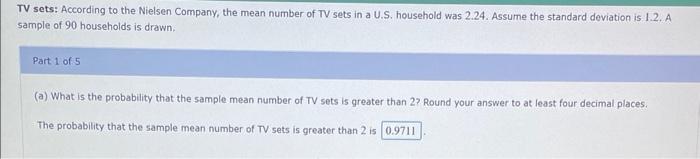
TV sets: According to the Nielsen Company, the mean number of TV sets in a U.S. household was \( 2.24 \). Assume the standard deviation is 1.2. A sample of 90 households is drawn. Part 1 of 5 (a) What is the probability that the sample mean number of TV sets is greater than \( 2 ? \) Round your answer to at least four decimal places. 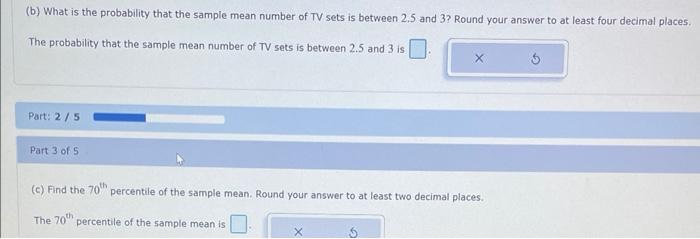The probability that the sample mean number of TV sets is greater than 2 is (b) What is the probability that the sample mean number of TV sets is between \( 2.5 \) and 3 ? Round your answer to at least four decimal places. The probability that the sample mean number of TV sets is between \( 2.5 \) and 3 is Part: \( 2 / 5 \) Part 3 of 5 (c) Find the \( 70^{\text {th }} \) percentile of the sample mean. Round your answer to at least two decimal places. 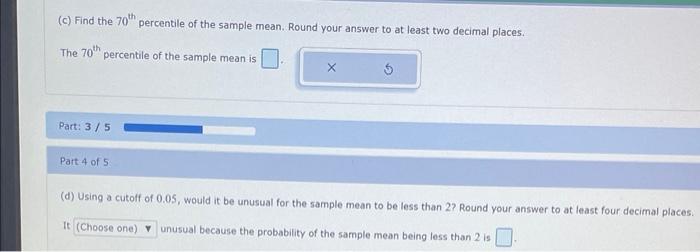The \( 70^{\text {th }} \) percentile of the sample mean is (c) Find the \( 70^{\text {th }} \) percentile of the sample mean. Round your answer to at least two decimal places. The \( 70^{\text {th }} \) percentile of the sample mean is Part: \( 3 / 5 \) Part 4 of 5 (d) Using a cutoff of \( 0.05 \), would it be unusual for the sample mean to be less than 2 ? Round your answer to at least four decimal places. It) unusual because the probability of the sample mean being less than 2 is