(Solved): Use integration to find a general solution of the differential equation \( \frac{d y}{d x}-\frac{17 ...

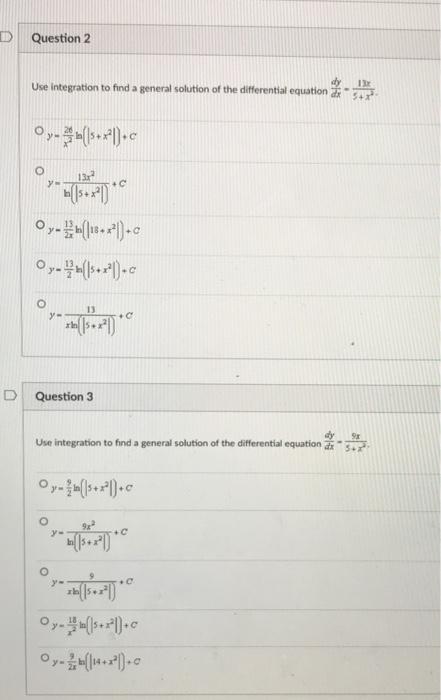
Use integration to find a general solution of the differential equation \( \frac{d y}{d x}-\frac{17 x}{5+x^{2}} \). \[ y=\frac{2 x}{x^{2}} \ln \left(\left|5+x^{2}\right|\right)+C \] \[ y=\frac{13 x^{2}}{k\left(\left|5+x^{2}\right|\right)}+C \] \[ \begin{array}{l} y=\frac{13}{2 x} \ln \left(\left|18+x^{2}\right|\right)+C \\ y=\frac{13}{2} \mathrm{k}\left(\left|5+x^{2}\right|\right)+C \end{array} \] \[ y=\frac{13}{x \ln \left(\left|5+x^{2}\right|\right)}+C \] Question 3 Use integration to find a general solution of the differential equation \( \frac{d y}{d x}=\frac{9 x}{5+x^{2}} \). 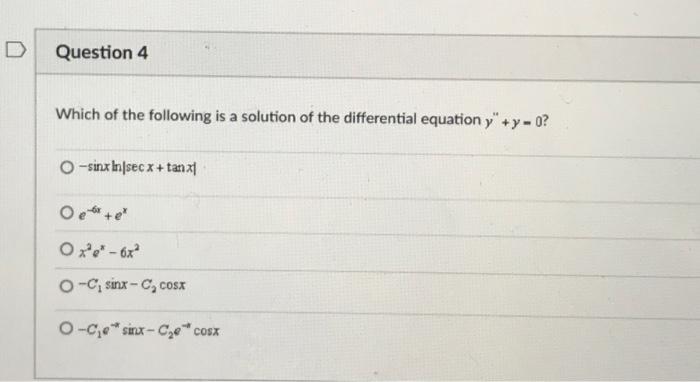\[ y=\frac{9}{2} \ln \left(\left|5+x^{2}\right|\right)+C \] \[ y=\frac{9 x^{2}}{\ln \left(\left|5+x^{2}\right|\right)}+C \] \[ y=\frac{9}{x k\left(5+x^{2}\right)}+C \] \[ y=\frac{10}{x^{2}} \ln \left(\left|5+x^{2}\right|\right)+C \] \[ \mid y=\frac{9}{2 x} h\left(\left|14+x^{2}\right|\right)+c \] Which of the following is a solution of the differential equation \( y^{\prime \prime}+y=0 \) ? \( -\sin x \ln |\sec x+\tan x| \) \( e^{-6 x}+e^{x} \) \( x^{2} e^{x}-6 x^{2} \) \( -C_{1} \sin x-C_{2} \cos x \) \( -C_{1} e^{-x} \sin x-C_{2} e^{-x} \cos x \)