(Solved): Use the method describe in class / text to solve the following Bernoulli equation: \( \frac{d y}{d ...

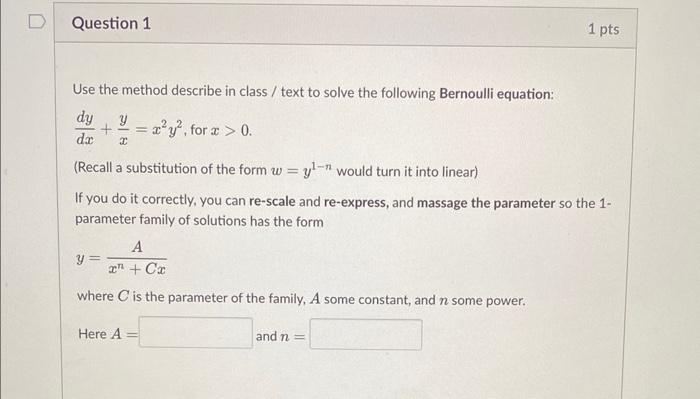
Use the method describe in class / text to solve the following Bernoulli equation: \( \frac{d y}{d x}+\frac{y}{x}=x^{2} y^{2} \), for \( x>0 \) (Recall a substitution of the form \( w=y^{1-n} \) would turn it into linear) If you do it correctly, you can re-scale and re-express, and massage the parameter so the 1parameter family of solutions has the form \[ y=\frac{A}{x^{n}+C x} \] where \( C \) is the parameter of the family, \( A \) some constant, and \( n \) some power. 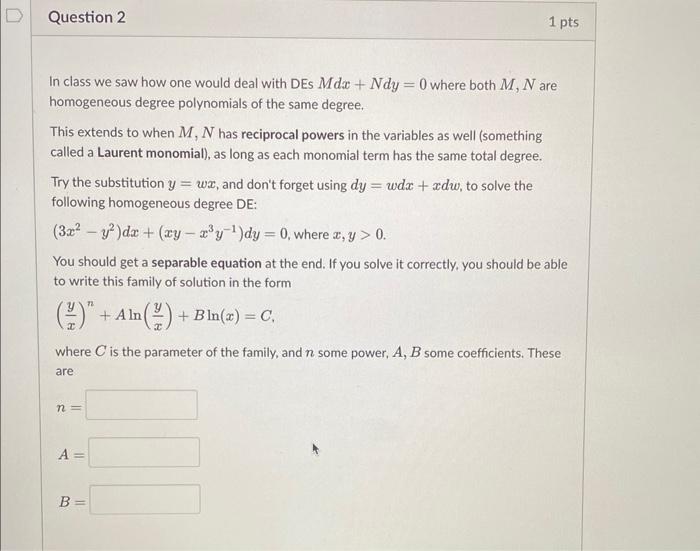Here \( A= \) and \( n= \) In class we saw how one would deal with DEs \( M d x+N d y=0 \) where both \( M, N \) are homogeneous degree polynomials of the same degree. This extends to when \( M, N \) has reciprocal powers in the variables as well (something called a Laurent monomial), as long as each monomial term has the same total degree. Try the substitution \( y=w x \), and don't forget using \( d y=w d x+x d w \), to solve the following homogeneous degree DE: \( \left(3 x^{2}-y^{2}\right) d x+\left(x y-x^{3} y^{-1}\right) d y=0 \), where \( x, y>0 \) You should get a separable equation at the end. If you solve it correctly, you should be able to write this family of solution in the form \[ \left(\frac{y}{x}\right)^{n}+A \ln \left(\frac{y}{x}\right)+B \ln (x)=C \] where \( C \) is the parameter of the family, and \( n \) some power, \( A, B \) some coefficients. These are \[ n= \] \[ A= \] \[ B= \]