(Solved): V0 = V2 so please solve for V2 with the given matrix. \( \mathrm{KCL} \) equations for ...

V₀ = V₂ so please solve for V2 with the given matrix.

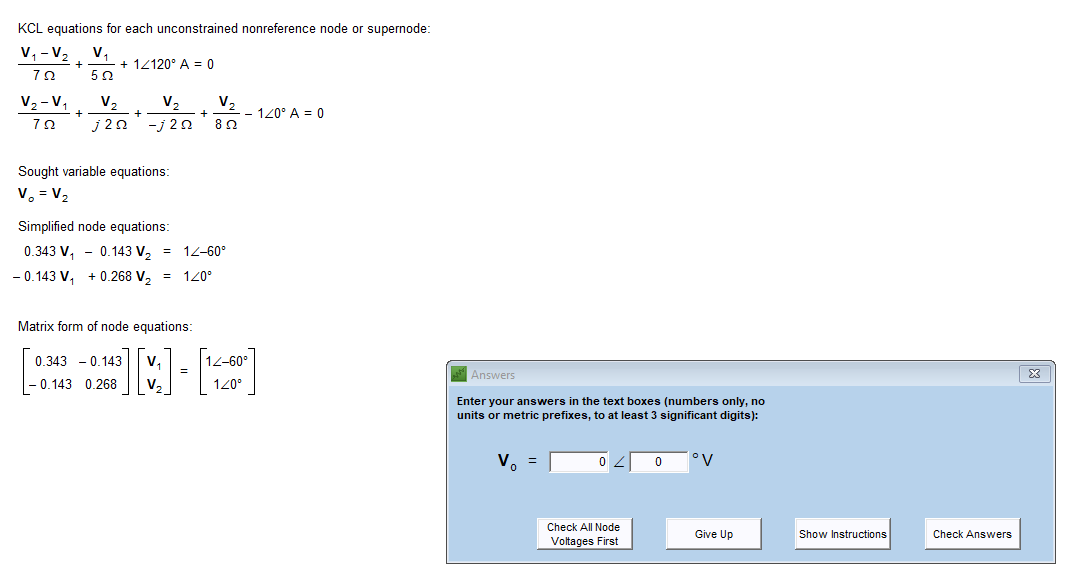
\( \mathrm{KCL} \) equations for each unconstrained nonreference node or supernode: \[ \begin{array}{l} \frac{\mathbf{V}_{1}-\mathbf{V}_{2}}{7 \Omega}+\frac{\mathbf{V}_{1}}{5 \Omega}+1 \angle 120^{\circ} \mathrm{A}=0 \\ \frac{\mathbf{V}_{2}-\mathbf{V}_{1}}{7 \Omega}+\frac{\mathbf{V}_{2}}{j 2 \Omega}+\frac{\mathbf{V}_{2}}{-j 2 \Omega}+\frac{\mathbf{V}_{2}}{8 \Omega}-1 \angle 0^{\circ} \mathrm{A}=0 \end{array} \] Sought variable equations: \[ \mathrm{V}_{\circ}=\mathrm{V}_{2} \] Simplified node equations: \[ \begin{aligned} 0.343 \mathrm{~V}_{1}-0.143 \mathrm{~V}_{2} &=1 \angle-60^{\circ} \\ -0.143 \mathrm{~V}_{1}+0.268 \mathrm{~V}_{2} &=1 \angle 0^{\circ} \end{aligned} \] Matrix form of node equations: \[ \left[\begin{array}{cc} 0.343 & -0.143 \\ -0.143 & 0.268 \end{array}\right]\left[\begin{array}{l} \mathbf{v}_{1} \\ \mathbf{v}_{2} \end{array}\right]=\left[\begin{array}{c} 1 \angle-60^{\circ} \\ 1 \angle 0^{\circ} \end{array}\right] \] Enter your answers in the text boxes (numbers only, no units or metric prefixes, to at least 3 significant digits): \[ \mathbf{V}_{0}= \] \( { }^{\circ} \mathrm{V} \)