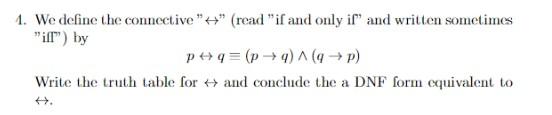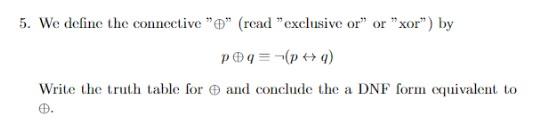(Solved): We define the connective " \( \leftrightarrow \) " (read "if and only if" and written someti ...

We define the connective " \( \leftrightarrow \) " (read "if and only if" and written sometimes "ifl") by \[ p \leftrightarrow q \equiv(p \rightarrow q) \wedge(q \rightarrow p) \] Write the truth table for \( \leftrightarrow \) and conclude the a DNF form equivalent to \( \leftrightarrow \) 5. We define the connective " \( \oplus \) " (read "exclusive or" or "xor") by \[ p \oplus q \equiv \neg(p \leftrightarrow q) \] Write the truth table for \( \oplus \) and conclude the a DNF form equivalent to \( \oplus \) 1. Use the associative laws (second question in this assignment) to explain the following: \[ \begin{array}{l} \left(p_{1} \vee p_{2}\right) \vee p_{3}=p_{1} \vee p_{2} \vee p_{3} \\ \left(p_{1} \wedge p_{2}\right) \wedge p_{3}=p_{1} \wedge p_{2} \wedge p_{3} \end{array} \] 2. Prove the De Morgan laws for 3 variables: Use the previous exercise (and the De Morgan laws for 2 variables) to prove \[ \begin{array}{l} \neg\left(p_{1} \vee p_{2} \vee p 3\right)=\neg p_{1} \wedge \neg p_{2} \wedge \neg p 3 \\ \neg\left(p_{1} \wedge p_{2} \wedge p_{3}\right)=\neg p_{1} \vee \neg p_{2} \vee \neg p_{3} \end{array} \] 3. The proposition \( R \) is given in the following truth table: (a) Write the DNF of \( R \) (b) Notice that \[ R \equiv \neg(p \wedge q \wedge r) \wedge \neg(p \wedge q \wedge(\neg r)) \] (meaning: \( R \) is True if we are \( \mathrm{NO}^{\prime} \mathrm{T} \) in line \( 1 * \mathrm{AND}^{*} \mathrm{NO} \mathrm{T} \) in line 2). Use De Morgan to turn this expression to the CNF of \( R \). 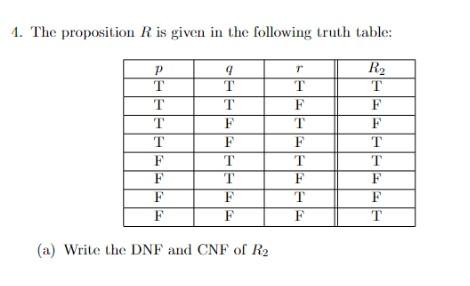1. The proposition \( R \) is given in the following truth table: (a) Write the DNF and CNF of \( R_{2} \)