(Solved): weights (in grams) were as follows. Use =0.01. (a) What is the level of significance? State the ...

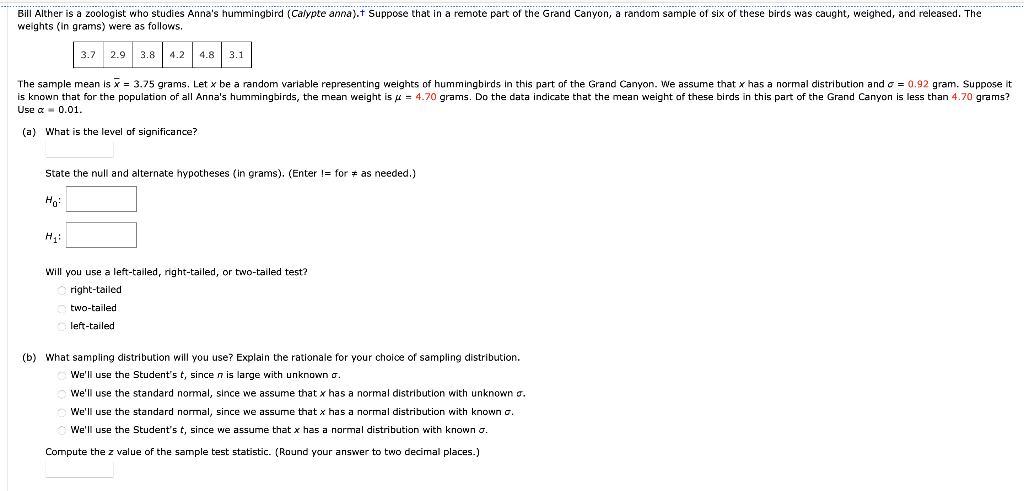
weights (in grams) were as follows. Use $\alpha =0.01$. (a) What is the level of significance? State the null and alternate hypotheses (in grams). (Enter $I=$ for $\ne$ as needed.) $H_0:$ $H_1\text{ : }$ Will you use a left-tailed, right-tailed, or two-tailed test? right-tailed two-tailed left-tailed (b) What sampling distribution will you use? Explain the rationale for your choice of sampling distribution. We'll use the Student's t, since $\pi$ is large with unknown $\sigma$. We'll use the standard normal, since we assume that $x$ has a normal distribution with unknown $\sigma$. We'll use the standard normal, since we assume that $x$ has a normal distribution with known $\sigma$. We'll use the Student's t, since we assume that $x$ has a normal distribution with known $\sigma$. Compute the $z$ value of the sample test statistic. (Raund your answer to two decimal places.) (c) Find the $P$-value. (Round your answer to four decimal places.) $\text{ P-value }=$ Sketch the sampling distribution and show the area corresponding to the P-value. (d) Based on your answers in parts (a) to (c), will you reject or fail to reject the null hypothesis? Are the data statistically significant at level $\alpha$ ? At the $\alpha =0.01$ level, we reject the null hypothesis and conclude the data are statistically significant. At the $\alpha =0.01$ level, we reject the null hypothesis and conclude the data are not statistically significant. At the $\alpha =0.01$ level, we fail to reject the null hypothesis and conclude the data are statistically significant. At the $\alpha =0.01$ level, we fail to reject the null hypothesis and conclude the data are not statistically significant. (e) State your conclusion in the context of the application. There is sufficient evidence at the 0.01 level to conclude that humming birds in the Grand Canyon weigh less than 4.70 grams. There is insufficient evidence at the 0.01 level to conclude that humming birds in the Grand Canyon weigh less than 4.70 grams.