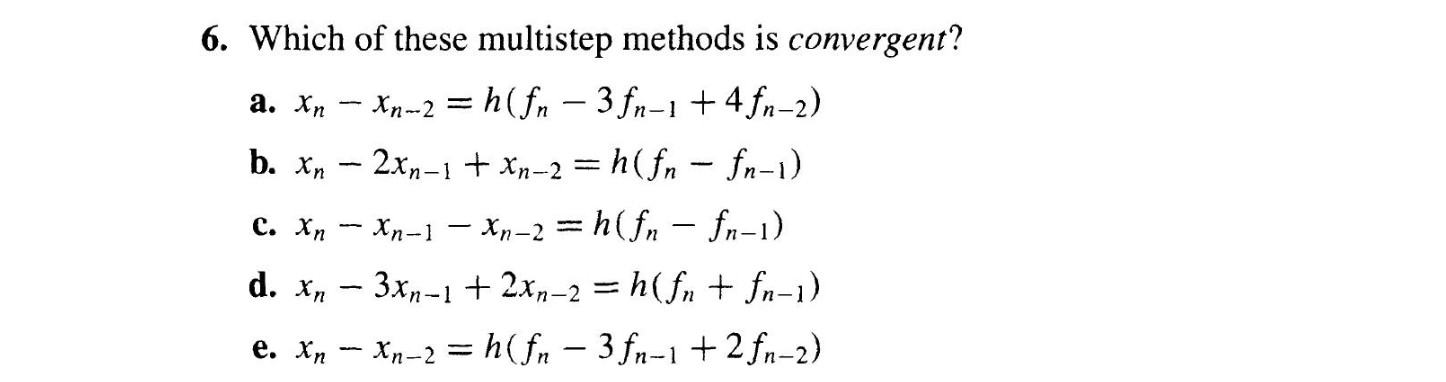Home /
Expert Answers /
Advanced Math /
which-of-these-multistep-methods-is-convergent-a-xnxn2-h-fn3fn1-4fn2-pa943
Expert Answer
To determine the convergence of the given multistep methods, we can use the concept of consistency and stability. A multistep method is said to be consistent if the local truncation error tends to zero as the step size h tends to zero. A method is stable if the errors in the solution remain bounded as h tends to zero.