(Solved): X92=11.070 (Round to three decimal places as needed) Delemine the rejection region. A. x2>x0 ...

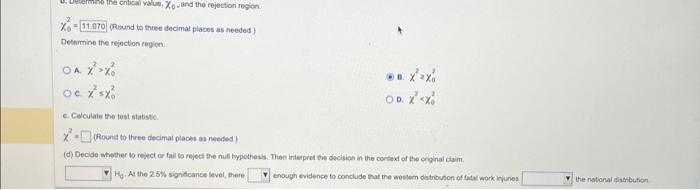
$X_9^2=11.070$ (Round to three decimal places as needed) Delemine the rejection region. A. $x^2>x_0^2$ c. $x^2\cdot x^2$ 0. $x^2=x_0^2$ D. $x^2<x_0^2$ c. Cacculate the test statste. $x^2$ - (Round to three decimal places as needed.) (d) Decide whethec to reject or fail to reject the nul hypothesis. Then interpred the decision in the context of the criginal ctaim. He. 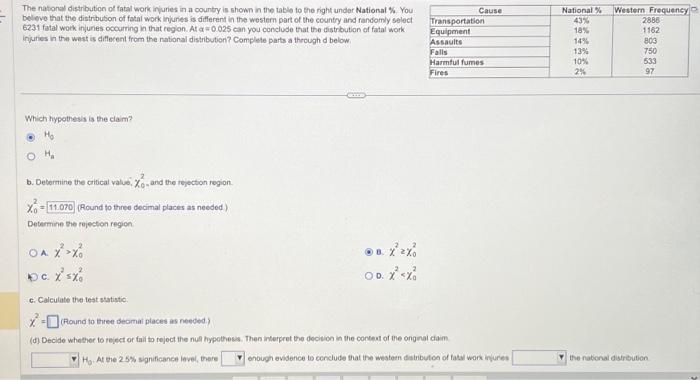At the $2.5\%$ signicance level, there Enough endence to conclvde that the weshom datrbubon of tatal work icyunes the nstonal istribution The natonal distrbution of fatal work injuries in a country is shown in the table to the right under National $\%$. You beleve that the distribution of fatal work injuries is different in the wostem part of the country and randomly select 6231 fatal work injunes ocourting in that reglon. At $\alpha =0.025$ can you conclude that the distribution of fatal work injuries in the west is diflecent frem the national distribution? Complete parts a through d below. Which hypothesis is the claim? ${\mathrm{H}}_6$ ${\mathrm{H}}_{\mathrm{a}}$ b. Debermine the critical value, $X_0^2$, and the rejection region. $X_0^2=11.070$ (Round to three decimal places as needed) Determine the rojection region A. $x^2>{\chi }_0^2$ B. ${\chi }^2\ge {\chi }_0^2$ c. $x^2=x_0^2$ D. ${\chi }^2<{\chi }_0^2$ c. Calculate the test statistic. $x^2=$ (Round to three deomal places as needed.) (d) Decide whether to reiect or fail to reject the nul hypothess. Then interpret the decivion in the contedt of the onginal daim Ho. At the $25\%$ significance lovel, there enough evisence to cenclude that the evestem ditributos of fatal work ipiree the rational distrbution