(Solved): yz=32 (b) Free-body diagram of the diving board A diving board (with \( 62 \mathrm{~cm} \) width an ...

yz=32

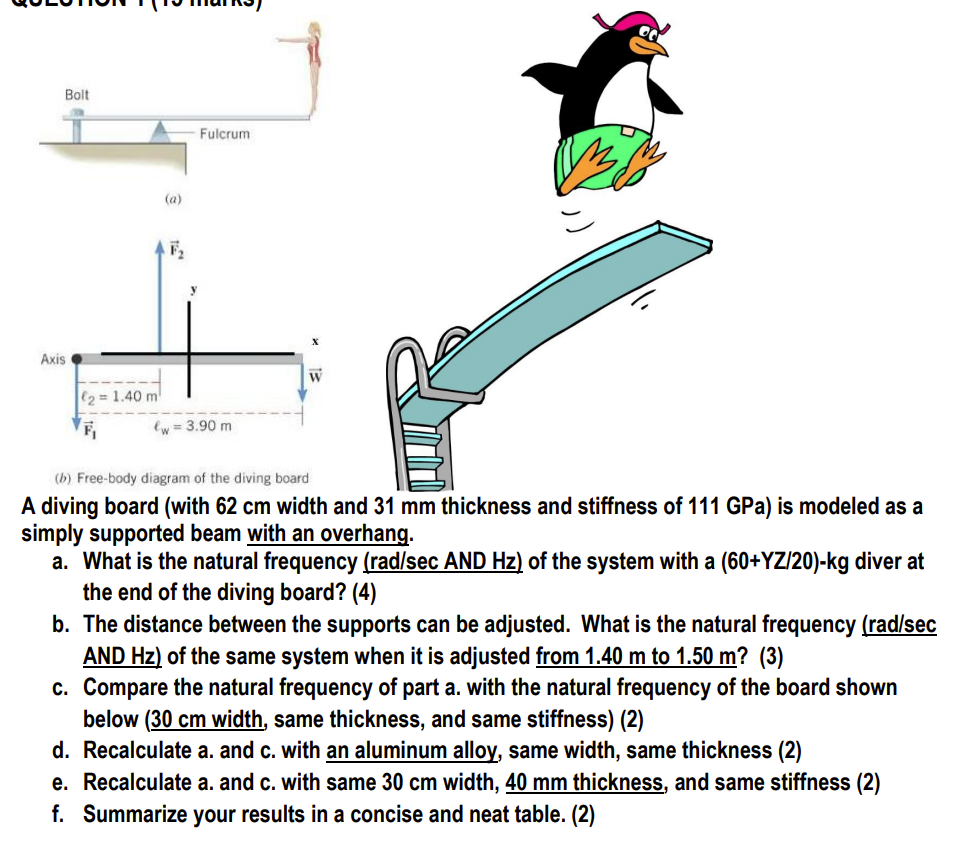
(b) Free-body diagram of the diving board A diving board (with \( 62 \mathrm{~cm} \) width and \( 31 \mathrm{~mm} \) thickness and stiffness of \( 111 \mathrm{GPa} \) ) is modeled as a simply supported beam with an overhang. a. What is the natural frequency \( (\mathrm{rad} / \mathrm{sec} \) AND Hz) of the system with a \( (60+Y Z / 20)-k g \) diver at the end of the diving board? (4) b. The distance between the supports can be adjusted. What is the natural frequency \( (\mathrm{rad} / \mathrm{sec} \) AND Hz) of the same system when it is adjusted from \( 1.40 \mathrm{~m} \) to \( 1.50 \mathrm{~m} \) ? (3) c. Compare the natural frequency of part a. with the natural frequency of the board shown below ( \( 30 \mathrm{~cm} \) width, same thickness, and same stiffness) (2) d. Recalculate a. and c. with an aluminum alloy, same width, same thickness (2) e. Recalculate a. and c. with same \( 30 \mathrm{~cm} \) width, \( 40 \mathrm{~mm} \) thickness, and same stiffness (2) f. Summarize your results in a concise and neat table. (2)